Характеристика роботи за розділами

1. Принцип дії системи

В цьому розділі для заданої системи автоматичного регулювання слід визначити функціональне призначення і принцип дії окремих елементів системи, встановити їх вхідні і вихідні величини. За принциповою схемою заданої системи автоматичного регулювання потрібно проаналізувати її роботу при зміні задаючої або збурюючої величини. На основі аналізу роботи системи та за принциповою схемою слід скласти функціональну схему системи і вказати величини, що діють на входах і виходах структурних ланок.

Рис. 2. Функціональна схема системи автоматичного регулювання температури в печі

Опис роботи системи автоматичного регулювання слід закінчити її класифікацією за різними ознаками.

2. Визначення передаточних функцій елементів системи

У випадку, коли задано диференціальне рівняння елемента системи, його передаточна функція визначається на основі перетворення Лапласа. Для цього вихідне диференціальне рівняння записують у операторній формі та знаходять відношення зображення вихідної величини до зображення вхідної величини при нульових початкових умовах. Якщо елемент системи має дві вхідні величини необхідно визначати дві передаточні функції за кожним із входів.

Нехай диференціальне рівняння об’єкта керування має вигляд

, /1/

де – вихідна величина; i – регулююча і збурююча дії. Знак мінус показує, що зі зростанням навантаження на об’єкт, регульована величина зменшується.

Покладемо, що вихідна величина має дві складові

/2/

Тоді рівняння /1/ розбивається на два рівняння. В операторній формі вони матимуть вигляд

/3/

/4/

де – зображення відповідних величин за Лапласом.

Рівнянням /3/ і /4/ відповідають передаточні функції об’єкта за каналом регулюючої величини

/5/

і за каналом збурення

. /6/

Структурна схема об’єкта наведена на рис. 3.

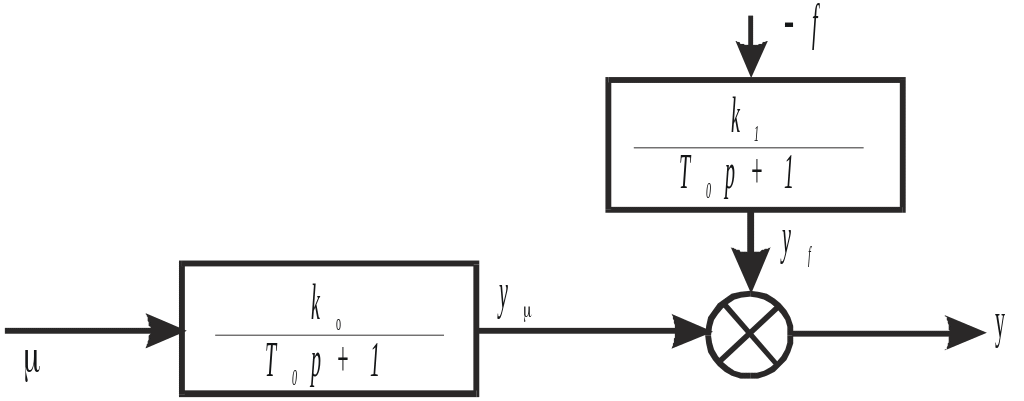
Рис. 3 Приклад структурної схеми об’єкта керування.

Аналогічним чином знаходять передаточні функції інших елементів системи.

Приклад. Рівняння, що описують роботу двигуна з редуктором:

- двигуна -

- редуктора - .

Ці два елементи являють собою послідовне з’єднання, результуюча передаточна функція якого буде мати вигляд:

,

де - вхідна величина,

- вихідна величина.

Операторна форма рівняння :

.

Передаточна функція двигуна з редуктором матиме вигляд:

_.

3. Структурна схема, передаточні функції і рівняння динаміки та статики системи

Структурну схему системи автоматичного керування будують на основі функціональної схеми, отриманої в розділі 1. При цьому функціональні елементи замінюють структурними ланками, з передаточними функціями отриманими в розділі 2. Приклад структурної схеми системи автоматичного регулювання температури рис. 4.

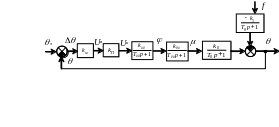
Рис. 4. Структурна схема системи автоматичного регулювання температури в печі.

Для знаходження передаточних функцій системи за каналами задаючої і збурюючої дії користуються правилами еквівалентних перетворень структурних схем. Спочатку, знаходять передаточну функцію розімкнутої системи. Так, як ланки ввімкнені послідовно, то передаточна функція розімкнутої системи знаходиться за формулою

/7/

де і - відповідно передаточні функції регулятора і об’єкта регулювання.

Передаточна функція замкнутої системи за каналом задаючої величини знаходиться через передаточну функцію розімкнутої системи за відомою формулою

/8/

Подібним чином знаходять і передаточну функцію системи за каналом збурення

/9/

де - передаточна функція каналу збурення об’єкта.

Щоб отримати диференціальні рівняння руху системи необхідно спочатку на основі передаточних функцій і записати диференціальні рівняння в операторній формі, а потім перейти до оригіналів функцій.

Рівняння статики отримують із відповідних рівнянь руху, прирівнюючи похідні усіх порядків до нуля.

Приклад. Передаточна функція розімкненої системи знаходиться за формулою

де і - відповідно передаточні функції регулятора і об’єкта регулювання.

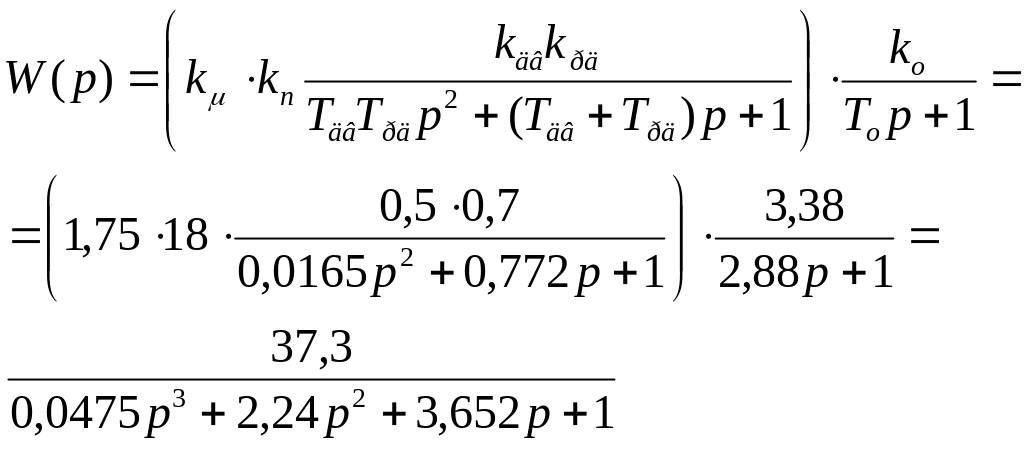
Передаточна функція замкнутої системи за каналом задаючої величини при одиничному зворотному зв’язку знаходиться через передаточну функцію розімкнутої системи.

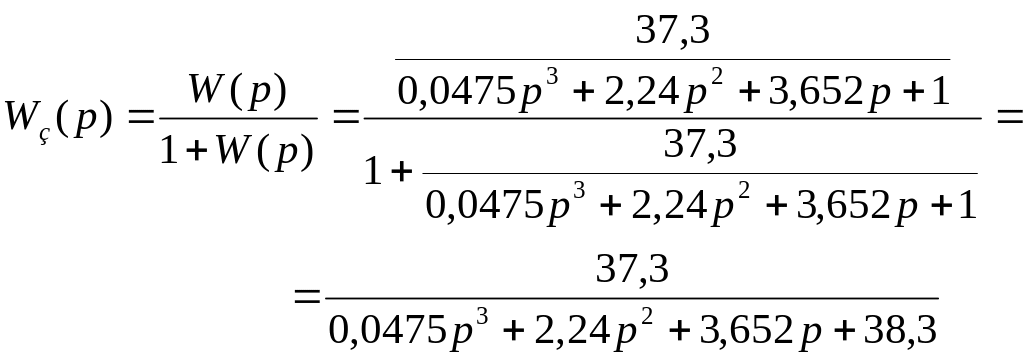
Диференціальні рівняння руху системи знаходимо, виходячи із означення передаточної функції системи:

;

;

Диференціальне рівняння руху системи за каналом завдання-вихід матиме вигляд:

;

А відповідне рівняння статики:

.

Передаточна функція системи за каналом збурюючої величини

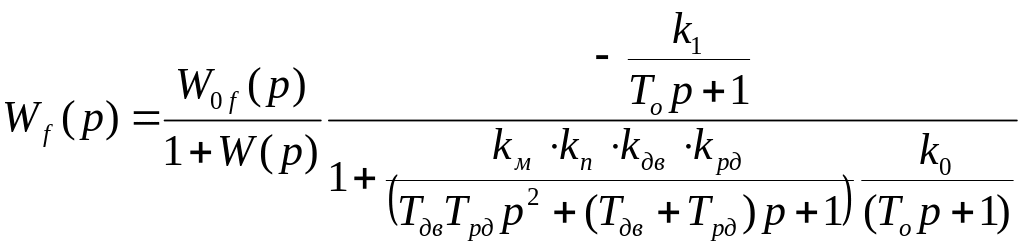
Підставимо значення, згідно варіанту:

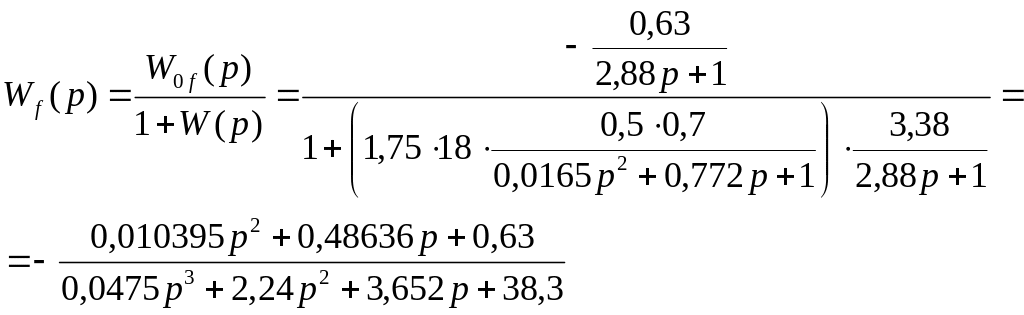
Знаходимо операторну форму диференційного рівняння, яке описує рух системи за каналом збурення-вихід:

Виконавши обернене перетворення Лапласа, одержимо:

Рівняння статики системи за каналом збурення: