Властивості коефіцієнта кореляції

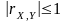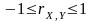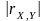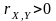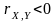1. ( ). Залежність між і тим „сильніша”, чим ближче до 1. Якщо при цьому , то із зростанням в середньому зростає і (додатна кореляція); якщо ж , то із зростанням величина в середньому спадає (від’ємна кореляція).

2. 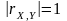тоді і тільки тоді, коли залежність між і лінійна, тобто існують такі числа і , при яких .

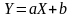3. Якщо випадкові величини і незалежні, то, очевидно, .

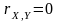4. Якщо 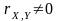, то випадкові величини і залежні.

Зауваження. Якщо , то кажуть, що між величинами і існує кореляційний зв’язок. Випадкові величини, для яких називаються некорельованими. Властивість 3 означає, що незалежні випадкові величини некорельовані, але рівність нулю коефіцієнта 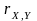є необхідною, але не достатньою умовою незалежності випадкових величин. З некорельованості випадкових величин у загальному випадку не випливає їх незалежність. Однак є випадки, коли незалежність випливає з некорельованості. Так буде, наприклад, у випадку нормально розподілених випадкових величин.

8. Умовні закони розподілу двовимірної випадкової величини та їх числові характеристики

Нехай задана двовимірна дискретна випадкова величина .

Означення. Умовним законом розподілу дискретної випадкової величини при фіксованому значенні випадкової величини 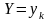називається множина можливих значень випадкової величини та відповідних їм умовних ймовірностей, обчислених при фіксованому значенні .

Умовний закон розподілу 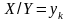у табличній формі запису має такий вигляд:

				...
				…

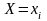
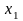
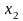
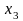
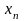
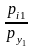
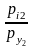
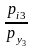
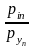
При цьому має виконуватися умова нормування:

.

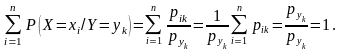
Числові характеристики для цього закону називають умовними.

Умовне математичне сподівання

Умовна дисперсія і умовне середнє квадратичне відхилення обчислюються відповідно за формулами:

.

.

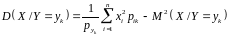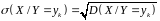Задачі для самостійного розв’язування

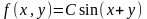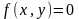1. Двовимiрна випадкова величина має щiльнiсть розподiлу в областi і по за областю. Знайти: 1) параметр С; 2) функцію розподілу системи; 3) 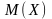та .

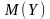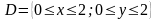2. Двовимiрна випадкова величина має щiльнiсть розподiлу в областi і по за областтю. Знайти умовні щільності розподілу складових системи. Встановити залежність чи незалежність випадкових величин та .

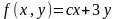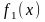3. Двовимiрна випадкова величина має щiльнiсть розподiлу в областi і по за областтю. Знайти: 1) параметр с; 2) та .

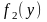4. Двовимiрна випадкова величина має щiльнiсть розподiлу 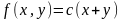в областi 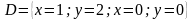і по за областтю. Знайти: 1) параметр с; 2) та .

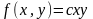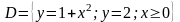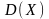5. Двовимiрна випадкова величина має щiльнiсть розподiлу в областi і по за областтю. Знайти: 1) параметр с; 2) та .

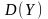6. Двовимiрна випадкова величина має щiльнiсть розподiлу в областi 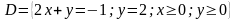і по за областтю. Знайти: 1) параметр с; та ; 3) та ; 4) .

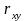7. Двовимiрну випадкову величину задано функцiєю розподiлу .

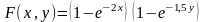
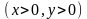Знайти щiльнiсть розподiлу 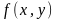i показати, що випадковi величини та незалежнi.

8. Дві незалежні випадкові величини 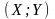задано їх законами розподілу:

, .

Знайти щільність розподілу та функцію розподілу системи випадкових величин .

9. Система випадкових величин розподілена зі сталою щільністю всередині квадрату зі стороною 4. Записати вираз для щільності розподілу та знайти функцію розподілу системи випадкових величин .

10. Система випадкових величин розподілена зі сталою щільністю всередині області 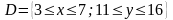і по за областю. Знайти: 1) ; 2) 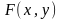; 3) , .

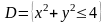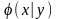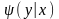11. Двовимiрна випадкова величина має щiльнiсть розподiлу в областi і по за областю. Знайти , , та . Визначити залежність, чи незалежність випадкових величин , а також їх корельованість.