
- •Тема 16 – 17. Багатовимірні випадкові величини. Система двох випадкових величин.
- •Література.
- •1. Поняття про багатовимірну випадкову величину
- •2. Функція розподілу двовимірної випадкової величини
- •Властивості :
- •5. Незалежність випадкових величин
- •6. Основні числові характеристики двовимірної випадкової величини
- •7. Коваріація випадкових величин. Коефіцієнт кореляції
- •Основні властивості коваріації:
- •Властивості коефіцієнта кореляції
- •8. Умовні закони розподілу двовимірної випадкової величини та їх числові характеристики
- •Задачі для самостійного розв’язування
Тема 16 – 17. Багатовимірні випадкові величини. Система двох випадкових величин.
Поняття про багатовимірну випадкову величину.
Функція розподілу двовимірної випадкової величини.
Двовимірні дискретні випадкові величини. Матриця розподілу.
Двовимірні неперервні випадкові величини. Сумісна щільність розподілу.
Незалежність випадкових величин.
Основні числові характеристики двовимірної випадкової величини.
Коваріація випадкових величин. Коефіцієнт кореляції.
Умовні закони розподілу двовимірної випадкової величини та їх числові характеристики..
Література.
Медведєв М.Г., Пащенко І.О. Теорія ймовірностей та математична статистика. Підручник. К.: Вид-во «Ліра-К». 2008 – 536 с.
Донченко В.С., Сидоров М. В.-С., Шарапов М.М. Теорія ймовірностей та математична статистика. Навчальний посібник. К.: Вид-во «Академія». 2009 – 286 с.
Гмурман В.Е. Теория вероятностей и математическая статистика. -М.: Высшая школа, 2004.—379 с.
1. Поняття про багатовимірну випадкову величину
Означення. Сукупність випадкових величин
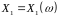 ,
,
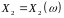 ,
…,
,
…,
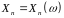 ,
,
які
задані на одному й тому самому ймовірнісному
просторі
 ,
називається багатовимірною
(
,
називається багатовимірною
( -вимірною)
випадковою
величиною,
системою
випадкових величин або
-вимірним
випадковим вектором.
-вимірною)
випадковою
величиною,
системою
випадкових величин або
-вимірним
випадковим вектором.
2. Функція розподілу двовимірної випадкової величини
Означення.
Функцією
розподілу ймовірностей (або сумісною
функцією розподілу)
двовимірної випадкової величини
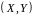 називається така функцію двох аргументів
називається така функцію двох аргументів
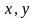 ,
яка визначає ймовірність сумісною появи
подій
,
яка визначає ймовірність сумісною появи
подій
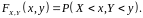
Подія
в дужках означає добуток подій:
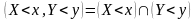 .
.
К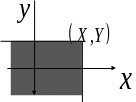 ористуючись
геометричною інтерпретацією двовимірної
випадкової величини
як
випадкової точки на площині, можна дати
геометричне тлумачення функції розподілу:
це є ймовірність влучення в нескінченний
квадрант з вершиною в точці
,
який лежить лівіше і нижче її:
ористуючись
геометричною інтерпретацією двовимірної
випадкової величини
як
випадкової точки на площині, можна дати
геометричне тлумачення функції розподілу:
це є ймовірність влучення в нескінченний
квадрант з вершиною в точці
,
який лежить лівіше і нижче її:
Властивості
функції розподілу
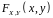 двовимірної випадкової величини
аналогічні властивостям одновимірної
випадкової величини:
двовимірної випадкової величини
аналогічні властивостям одновимірної
випадкової величини:
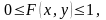 оскільки
оскільки
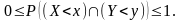
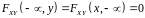 .
.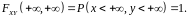
Функція
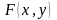 неспадна по кожному аргументу
неспадна по кожному аргументу і
і
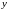 .
.Функція неперервна зліва в будь-якій точці
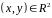 по кожному аргументу.
по кожному аргументу.Ймовірність попадання точки
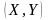 в довільний прямокутник
в довільний прямокутник
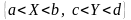 дорівнює
дорівнює
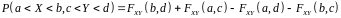
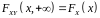 ,
,
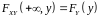 ,
тобто якщо один із аргументів
прямує до
,
тобто якщо один із аргументів
прямує до
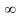 ,
то функція розподілу системи прямує
до функції розподілу того аргументу,
що не прямує до
.
,
то функція розподілу системи прямує
до функції розподілу того аргументу,
що не прямує до
.
Остання
властивість встановлює природний
зв'язок між функцією розподілу
двовимірної випадкової величини і
функціями розподілу
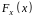 і
і
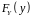 (які також називають частинними)
одновимірних випадкових величин
(які також називають частинними)
одновимірних випадкових величин
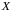 і
і
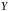 .
.
3. Двовимірні дискретні випадкові величини
Матриця розподілу
Означення. Двовимірна випадкова величина називається дискретною, якщо кожна з випадкових величин і дискретна.
4. Двовимірні неперервні випадкові величини
Сумісна щільність розподілу
Означення. Двовимірна випадкова величина називається неперервною (точніше, абсолютно неперервною), якщо її функцію розподілу можна зобразити у вигляді збіжного невластивого інтегралу

Функція
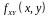 ,
як і в одновимірному випадку, називається
щільністю
розподілу ймовірностей
випадкової
величини
.
Функція
може існувати за умови, що
є неперервною за аргументами
і
та двічі диференційованою.
,
як і в одновимірному випадку, називається
щільністю
розподілу ймовірностей
випадкової
величини
.
Функція
може існувати за умови, що
є неперервною за аргументами
і
та двічі диференційованою.
Очевидно, що в точках неперервності
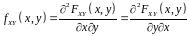 .
.
