3 Типовые задачи

В этом разделе приведены типовые задачи различного уровня сложности, сгруппированные по видам вычислительных процессов. Числовые значения исходных данных даны для тестирования, либо решения задачи на компьютере. При составлении алгоритма их можно игнорировать.

3.1 РазветвляющиЕся вычислительныЕ процессЫ

Задача 1. На плоскости расположена окружность радиуса R с центром в начале координат. Ввести заданные координаты точки и определить, лежит ли она на окружности. Результат присвоить символьной переменной. Решить задачу при R=2 для точек с координатами (0;2), (-1,5;0,7), (1;1), (3;0).

 Считать , что точка с координатами (x,y) лежит на окружности радиуса R, если , где - точность, с которой осуществляется проверка на равенство.

Задача 2. Определить, принадлежит ли заданная точка фигуре, представленной на рисунке. Решить задачу для точек с координатами (-0,5;0,8), (0,5;0,4).

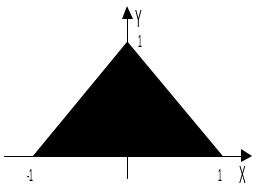
 Уравнение прямой, ограничивающей фигуру слева: y=1+x (x<0), справа: y=1-x (x0). Следовательно, точка принадлежит фигуре, если у0 и y+x1.

Задача 3. Определить, принадлежит ли точка фигуре, представленной на рисунке. Решить задачу для точек с координатами (0,2;0,3), (-2,5;0,4), (1,5;-0,2).

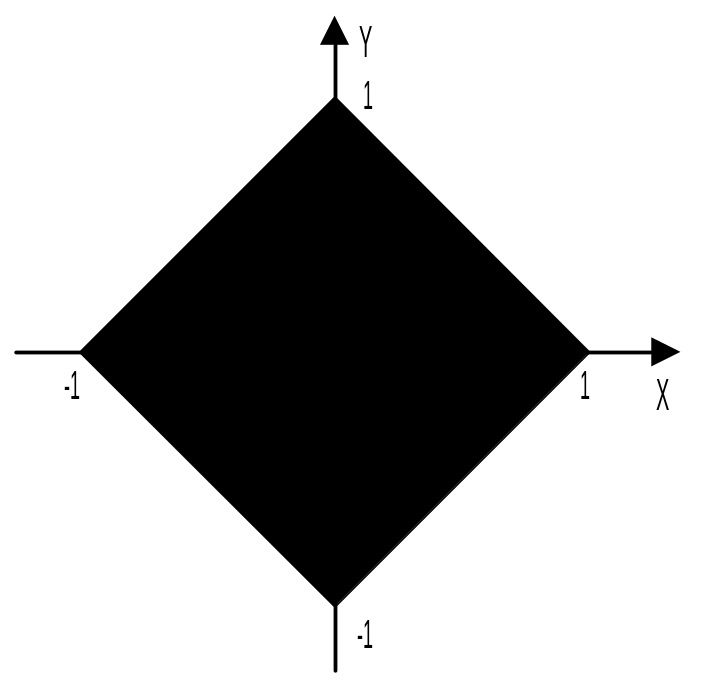
 Точка принадлежит фигуре, если y+x1.

Задача 4. Заданы координаты двух точек. Определить, лежат ли они на одной окружности с центром в начале координат. Результат присвоить символьной переменной. Задачу решить для точек с координатами (0;2), (2;0), (1;3), (2;2).

 Две точки лежат на одной окружности, если длины радиус-векторов, соединяющих эти точки с началом координат, равны. Проверку на равенство осуществлять с точностью .

Задача 5. Заданы площади круга R и квадрата S. Определить, поместится ли квадрат в круге. Задачу решить при :

1) R=70, S=36.74; 2) R=0.86, S=0.64.

 Квадрат поместится в круге, если диагональ квадрата меньше или равна диаметру окружности.

Задача 6. Заданы площади круга R и квадрата S. Определить, поместится ли круг в квадрате. Задачу решить при:

1) R=3.2, S=3.5; 2) R=3.2, S=4; 3) R=6, S=9.

Задача 7. Составить алгоритм для определения подходящего возраста кандидатуры для вступления в брак, используя следующее соображение: возраст девушки равен половине возраста мужчины плюс 7, возраст мужчины определяется как удвоенный возраст девушки минус 14. Данные для тестирования и проверки работы задать самостоятельно.

Задача 8. Составить алгоритм, реализующий эпизод сказки: спрашивает, куда предпочитает пойти герой (налево, направо или прямо), и печатает, что его ждёт в каждом случае. Ответ напечатать в символьном виде. Текст вопросов и ответов задать самостоятельно.

Задача 9. В киоске продаётся газета стоимостью 50 коп. и журнал стоимостью 3 руб. 20 коп. Составить алгоритм, который спрашивает о желании покупателя (журнал или газета?), принимает деньги (сумма денег вводится с клавиатуры) и печатает причитающуюся сдачу.

Задача 10. В продаже книг в книжном магазине принимает участие ЭВМ. Составить алгоритм программы, которая запрашивает стоимость книг; сумму денег, внесённую покупателем, а далее определяет причитающуюся сдачу (если денег внесено больше), печатает "спасибо", если сдачи не требуется, или выдаёт сообщение о недостаточности внесённой суммы. Исходные данные задать самостоятельно.

Задача 11. В ЭВМ поступают результаты соревнований по плаванию для трёх спортсменов. Выбрать и напечатать лучший результат. Решить задачу для следующих наборов данных:

1) 11,3; 10,6; 11; 2) 10; 10,9; 13; 3) 16; 18; 13.

Задача 12. Определить, принадлежит ли точка D треугольнику АВС. Треугольник задан координатами своих вершин. Решить задачу при А(2;2), В(4;5), С(7;3) и

1) D(4;3), 2) D(6;4,5), 3) D(3;4).

 Прямая, отрезком которой является сторона треугольника, делит плоскость на две полуплоскости. Если заданная точка и противоположная этой стороне вершина находятся в разных полуплоскостях, то точка не может принадлежать треугольнику. Проверив это условие для всех трех сторон, можно определить, лежит ли точка внутри или вне треугольника.

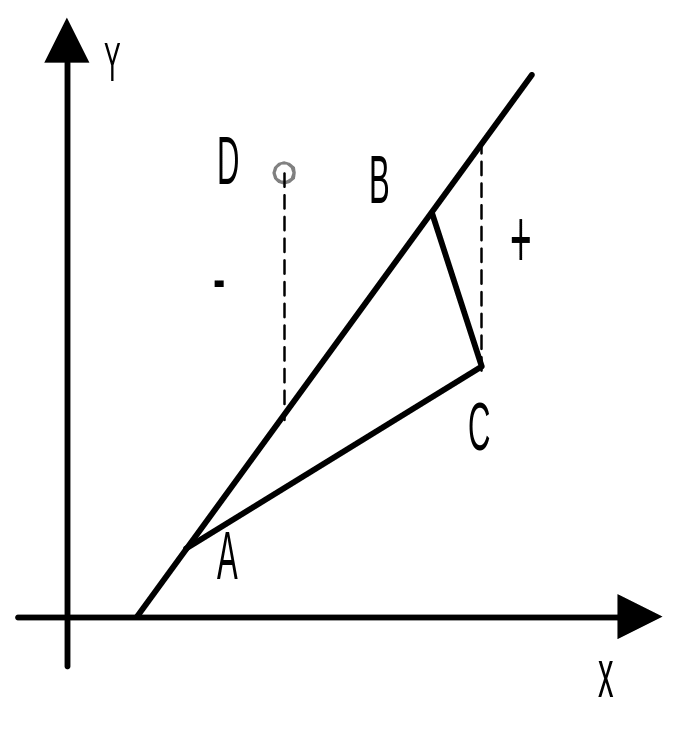
Прямая, проходящая через вершины A(A₁,A₂) и B(B₁,B₂) описывается уравнением (B₁-A₁)/(B₂-A₂)= =(B₁-x)/(B₂-y), определяющим зависимость y=f(x). Если заданная точка D(D₁,D₂) и противоположная вершина C(C₁,C₂) лежат по разные стороны от этой прямой, то произведение (f(D₁)-D₂)(f(C₁)-C₂) будет отрицательным, так как его сомножители имеют отрицательные знаки. Если для всех трех сторон произведения неотрицательные, то точка принадлежит треугольнику.

Задача 13. Найти действительные корни квадратного уравнения вида . Если действительных корней нет, то выдать соответствующее сообщение.

Задача 14. Из величин, определяемых арифметическими выражениями a=sin x, b=cos x, c=ln|x| при заданном x, определить и вывести на печать минимальное значение.

Задача 15. При обжиге посуды температура печи должна быть 1000 С. Если температура отличается от заданной не более, чем на 1 процент, получим изделия 1 сорта, если больше - изделия 2 сорта. Рассчитать сортность изделий при температуре печи 1007 С.

Задача 16. Определить и вывести на печать номер квадранта, в котором расположена точка М(x,y).

Задача 17. Сравнить между собой значения величин x и y. Вывести на печать результат сравнения в виде “x>y”, “x<y” или “x=y”.

Задача 18. Определить, какая из двух фигур - круг или квадрат - имеет большую площадь. Известно, что сторона квадрата равна а, радиус круга r. Вывести на печать название и значение площади большей фигуры.

Задача 19. Найти первое отрицательное число в заданной числовой последовательности а₁, а₂...а₇. Вывести на печать номер и значение первого отрицательного элемента или сообщение о том, что в заданной числовой последовательности отрицательных чисел нет.

Задача 20. Вычислить значение функции: