1.2. Уравнивание триангуляции 2-го разряда,
1.2.1 Исходные данные.
По результатам предвар1ггельных вычислений (см. таблицу 5) и исходным данным
(см. таблицу 1) выполнить уравнение сете (см. таблицу 3).
Уравнение триангуляции 2-го разряда обычно производят упрощенным коррелатным
способом, как более простым дай вычислений, но дающим достаточно надежные
результаты.
1.2.2. Порядок вычислений.
1.2.2.1. В ведомость уравновешивания (таблица б) со второй рабочей схемы (см. рисунок 3) выписываем углы (графа 3) в том же порядке, как и в предварительном решении треугольников.
Уравновешивание углов и окончательное решение треугольников
№ треугольника |
|
Приведенные углы i |
Поправки первичные
|
Предварительные исправленные углы
|
Попр-ки Вторичные (i)``
|
Уравненные Окончательно углы i`` |
Синусы углов I``
|
Стороны s(M)
|
|||||||
(i)1|
|
(i)1|
|
(i)1
|
|||||||||||||
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10 |
11 |
|||||
|
|
2 3 1
|
39 25 39 59 23 55 81 10 16
|
+3 ‘’ +4’’ +3’’ |
+2’’ -3’’ +1’’ |
+5’’ +1’’ +4’’
|
39 25 44 59 23 56 81 10 20
|
+3’’ - -3’’
|
39 25 47 59 23 56 81 10 17
|
8919.09 0.635132 0.860732 0.988152 |
1854.01 5212.55 2884.50
|
|||||
|
|
179 59 50 Wi= |
+10 -10
|
0 |
+10 |
180 00 00 |
0 |
180 00 00 |
3533.39
|
|
|||||
||
|
5 6 4
|
54 43 03 94 43 05 30 33 32 |
+6’’ +7’’ +6’’
|
+2’’ -3’’ +1’’ |
+8’’ +4’’ +8’’ |
54 43 11 97 43 09 30 33 40
|
+6’’ - -6’’ |
54 43 17 94 43 09 30 33 34 |
0.816354 0.996612 0.508432 |
2884.50 3521.42 1796.49 |
|||||
|
|
179 59 40 Wi= |
+20 -20 |
0 |
+20 |
180 00 00 |
0 |
180 00 00 |
2367.85
|
|
|||||
|||
|
8 9 7
|
49 20 48 89 27 26 41 11 33 |
+4’’ +5’’ +4’’ |
+2’’ -3’’ +1’’ |
+6’’ +2’’ +5’’ |
48 20 54 89 27 28 41 11 38 |
+5’’ - -5’’
|
49 20 59 89 27 28 41 11 33 180 00 00 |
0.758700 0.999955 0.658591 |
1796.49 2367.74 1559.44 |
|||||
|
|
179 59 47 Wi= |
+13 -13 |
0 |
+13 |
180 00 00 |
0 |
180 00 00 |
3244.53 |
|
|||||
||||
|
11 12 10
|
28 43 30 116 25 34 34 51 06 |
-3’’ -3’’ -4’’ |
+2’’ -4’’ +2’’ |
-1’’ -7’’ -2’’ |
28 43 29 116 25 27 34 51 04 |
+8’’ - -8’’ |
28 43 37 116 25 27 34 50 56 |
0.480636 0.895533 0.571414
|
1559.44 2905.59 1853.37 |
|||||
|
|
180 00 10 Wi= |
-10 +10 |
0 |
-10 |
180 00 00 |
0 |
180 00 00 |
|
|
|||||
1.2.2.2. Составляем условные уравнения и вычисляем первичные поправки: их первые части (i) - (за условие фигур) и вторые - ( i )1 (за условие горизонта). Первые части первичных поправок (I )г вычисляем по формуле:
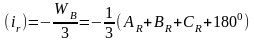(11)
где WR- невязка R - го треугольника.
AR , BR , CR -внутренние углы R-треугольника.
Т.е. в каждом треугольнике получают поправку на угол как одну треть невязки за
условие фигуры с противоположным знаком
Пример: Для первого треугольника (см. табл. 6) будем иметь:
(1)i = (2)i = (3)I = +3.3’’
Поправки округляют до целых секунд так, чтобы их сумма была равна невязке с противоположным знаком :
(1)i = +3’’ ; (2)i = +3’’ ; (3)I = +4’’
Так находят первичные поправки в каждом треугольнике (см. табл. 6)
1.2.2.3. Вычисляем предварительно исправленные углы при центральном пункте «Луговое»:
3’ i =3+(3)’ i
6’ i = 6=(6)’ i
9’ I = 9=(9)’ i
12’ I = 12=(12)’ i
1.2.2.4. Полученные углы выписываем в отдельную таблицу (таблица 7);
подсчитываем их сумму и вычисляем невязку W за условие горизонта по формуле:
(12)
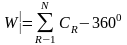
где CR - углы при центральном пункте «Луговое» Для предложенной схемы триангуляции
WR|=3|+6|+9|+12|-360˚
Значение WR| не должно превышать величины
(13)
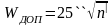
где n- число центральных углов CR( число треугольников)
Если WR ≤ WДОП то вычислить вторые части первичных поправок промежуточных (при центральном пункте) углов по формуле:
(14)
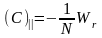
которые с округлением записываем в таблицу 7 и графу 5 таблицы б.
Пример:
(3)’ii = (6)’ii = (9)’ii = (12)’ii = -3’’.2
Округлив величину поправок до 1’’, получим :
(3)’ii = -3’’; (6)’ii = -3’’; (9)’ii = -3’’; (12)’ii = -4’’
1.2.2.5. Чтобы не нарушить ранее выполненных условий фигур, в каждый из связывающих углов треугольника также вводам поправки в размере половины поправки за условие «горизонта» в промежуточный угол при центральной точке, но с противоположным знаком.
(1)’ii = (2)’ii = ½ (3)’ii:
(4)’ii = (5)’ii = ½ (6)’ii:
Пример:
Для углов первого треугольника вторые поправки будут:
(3)’ii = -3’’,
(1)’ii = (2)’ii = + 3/2 = 1.5’’.
Округлить значение поправок до целых секунд с таким расчётом, чтобы сумма вторых поправок была равна нулю (граф 5, табл.6):
(1)’ii = +1’’ ; (2)’ii = +2’’.
Аналогично определять вторые поправки для остальных треугольников
Таблица 7
№№ углов
|
Центральные углы, исправленные по поправкам (C) |
|
Поправки (С) ˝
|
3 6 9 12 |
59 23 59 94 43 12 89 27 31 116 25 31
|
-3’’ -3’’ -3’’ -4’’ |
|
360 00 13’’ W’r = +13’’ |
-13’’ |
1.2.2.6. Находим первичные поправки ( I )΄ (см. графа 6. таблица 6), как сумму первых и вторых поправок:
(i)΄= (i)΄||+ (i)΄||
1.2.2.7. Вычисляем предварительно исправленные углы, введя в них первичные поправки (i)΄ и записываем их в графу 7.
Например, для первого треугольника получим
1’ = 1 + (1)’ ; 2’ = 2 + (2)’ и 3’ = 3 + (3)’.
Контролем решения для каждого треугольника служит равенство : сумма первичных поправок должна быть равна невязке с обратным знаком, а сумма углов – 180
1.2.2.8. Для определения вторичных поправок (за условие полюса) выписать в таблицу 8 1в первично исправленных углов, при этом в левую часть (графы 1,2) выписывают 1§ углов А (1,4,7,10), в правую часть (графы 4,5) -1§ углов В (2,5,8,11).
Таблица 8