4.2. Уравнение Лагранжа и дифференциальные уравнения электромеханических систем управления (эмсу)

Математические модели технических средств, систем автоматизации и управления весьма многообразны и могут быть достаточно сложными. В частности на сложность электромеханических систем управления влияет множество факторов: число, тип и последовательность звеньев (кинематических пар), компоновочные схемы размещения приводов механических подсистем и конструкции передаточных механизмов, наличие устройств уравновешивания и динамической развязки движений и др.

Механические системы, как правило, имеют значительно большую инерционность по сравнению с инерционностью электромагнитных цепей электроприводов, приводящих их в движение, что позволяет при составлении математических моделей ЭМСУ использовать уравнения Лагранжа 2-го рода [2]:

, (4.1)

где q, , – векторы обобщенных координат, скоростей и обобщенных сил;

– кинетическая энергия механической системы;

Решение уравнения (4.1), т. е. математическую модель механического объекта управления представляют в форме системы обыкновенных дифференциального уравнений (ОДУ), разрешенных относительно вторых производных обобщенных координат (обобщенных ускорений), т. е.

. (4.2)

Для составления уравнений Лагранжа составляют расчетную схему механической системы, учитывающую геометрические размеры механических звеньев, тип и распределение (порядок расположения) кинематических пар, массы звеньев, упругие свойства кинематических связей.

Составление дифференциальных уравнений движения материальной системы на основе уравнений Лагранжа проводят в следующей последовательности:

1. определяют число n степеней свободы материальной системы;

2) выбирают систему координат и вводят независимые обобщенные координаты q₁, q₂ ,…, q_n ; - вектор обобщенных координат; их число должно быть равно числу n степеней свободы механической системы;

примечание: обобщенные координаты – независимые параметры, однозначно определяющие положение точек материальной системы;

3) определяют обобщенные силы системы Q₁, Q₂,…, Q_n; - вектор обобщенных сил;

примечание 1: для определения обобщенной силы Q_i, соответствующей i-й обобщенной координате, надо вычислить сумму работ всех активных сил, включая реакции неидеальных связей, на обобщенном возможном перемещении ; при этом все остальные обобщенные возможные перемещения принимают равными нулю; тогда

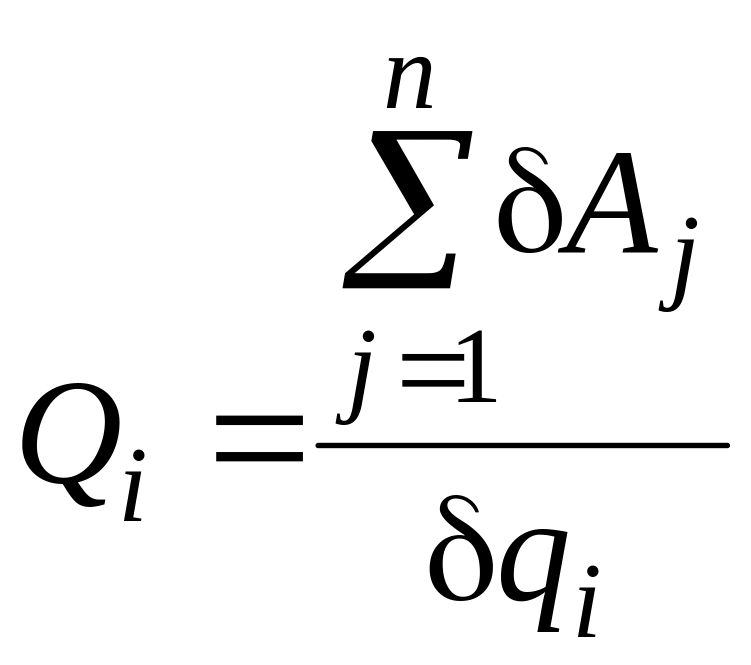; (4.3)

примечание 2: если силы, действующие на систему потенциальны (однозначно определяются только положением материальных точек системы), то обобщенную силу Q_i можно найти как частную производную потенциальной энергии по обобщенным координатам, т. е.

, (4.4)

где потенциальная энергия системы E_п определяется как функция обобщенных координат, т. е. ; потенциальная энергия, создаваемая силами тяжести звеньев механической системы, для i-го звена массой m_i равна , где - высота подъема центра масс i-го звена, g – ускорение силы тяжести; потенциальная энергия, создаваемая силами упругости упругого звена (например, пружины), для i-го звена равна , где с_i – жесткость упругого звена, - угол закручивания (приращение обобщенной координаты);

4) вычисляют кинетическую энергию E_к системы как функцию обобщенных координат и скоростей т. е. ; кинетическая энергия материальной системы определяется как сумма кинетических энергий всех n материальных точек системы

. (4.5)

Использование формулы (4.5) ориентировано на концепцию распределенных масс механической системы и требует определения абсолютных скоростей достаточно большого множества материальных точек системы с массами m_i .

Кинетическая энергия в частных случаях движения твердого тела:

- при поступательном движении: , где m – масса твердого тела, v – скорость любой его точки;

- при вращательном движении вокруг неподвижной оси: , где J_Z – момент инерции твердого тела относительно оси Z вращения, – угловая скорость вращения;

- при вращательном движении вокруг неподвижной точки: , где J – момент инерции твердого тела относительно мгновенной оси вращения, – модуль мгновенной угловой скорости;

Если в твердом теле удается выделить оси материальной симметрии и, соответственно, главные центральные оси инерции, то кинетическую энергию тела определяют по формуле

, (4.6)

где - осевые моменты инерции твердого тела;

- проекции мгновенной угловой скорости на соответствующие координатные оси.

5) находят частные производные кинетической энергии по обобщенным скоростям т. е. , а затем вычисляют их производные по времени:

;

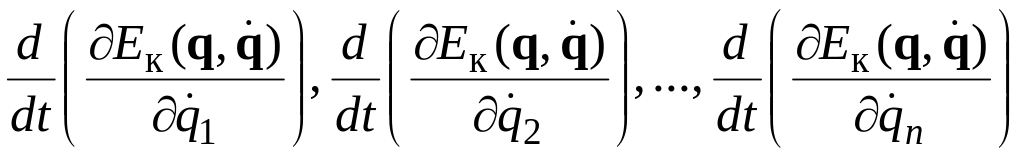6) находят частные производные кинетической энергии по обобщенным координатам т. е. ;

7) полученные в п. п. 3-6 результаты подставляют в уравнение (4.1) и дифференциальные уравнения разрешают относительно вторых производных по времени обобщенных координат, т. е. записывают уравнение движения механической системы в форме (4.2).

В качестве примера рассмотрим расчетную схему механизма с тремя степенями подвижности, приведенную на рис. 4.1. Такие схемы применяются для механизмов переносных движений роботов-манипуляторов, портальных кранов, экскаваторов, ротационных стендов и т. п.

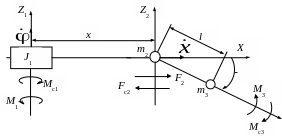
Рис. 4.1. Расчетная схема механизма с тремя степенями подвижности

Платформа механизма совершает вращательное движение вокруг оси Z₁ со скоростью . Каретка (ползун) массой m₂ перемещается вдоль радиуса

вращения платформы (оси X) со скоростью . Груз (изделие) массой m₃ поворачивается вокруг оси Y (ось Y направлена касательно к радиусу x вращения каретки, проходит через центр ее масс m₂) и отстоит на расстоянии от оси вращения.

1) В число обобщенных координат механизма включим угол  поворота платформы против часовой стрелки, радиус x перемещения каретки от оси вращения платформы и угол  поворота ИП вокруг оси X₂ против часовой стрелки, т. е. .

2) Будем полагать, что приведенный к валу платформы момент инерции равен , а массы m₂ радиально перемещаемой каретки и m₃ перемещаемого груза сосредоточены в их центрах масс.

3) Вектор обобщенных сил, действующих на систему (см. рис. 4.1),

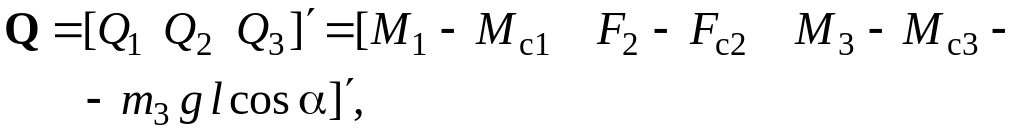(4.7)

где M₁, M₃ – вращающие моменты электроприводов на валах платформы и груза,

M_с1, M_с3 – реактивные моменты сопротивления на валах платформы и груза,

- активный момент сопротивления вращению груза, вызванный силой тяжести груза,

F₂, F_с2 – сила радиального перемещения каретки и сила сопротивления этому перемещению (см. рис. 4.1).

4) Кинетическую энергию стенда представим в виде суммы кинетических энергий платформы, каретки и груза, т. е.

, (4.8)

где ; (4.9)

– момент инерции платформы, включающей приведенный к ее валу момент инерции электропривода платформы;

; (4.10)

, (4.11)

где – абсолютные скорости центров масс соответственно каретки и платформы.

Каретка (ползун) совершает сложное движение и абсолютная скорость движения ее центра масс состоит из переносного вращательного движения платформы и относительного движения каретки вдоль оси X ее линейного перемещения, т. е.

а, следовательно,

. (4.12)

Груз совершает также сложное движение и скорость движения его центра масс состоит рассмотренного выше переносного сложного движения каретки и относительного движения груза вокруг оси Y. Применяя теорему о сложении скоростей точки к точечной массе m₃, получим

,

а, следовательно, 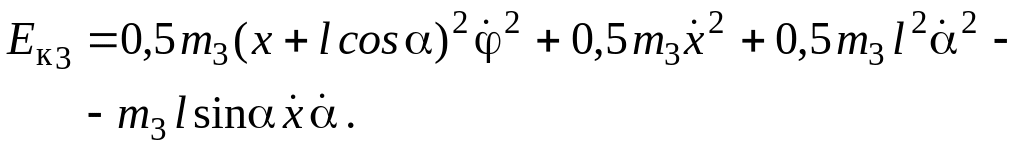(4.13)

Подставляя полученные выражения в (4.23), получим

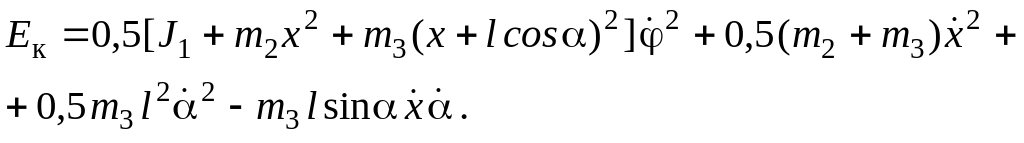(4.14)

5) Частные производные кинетической энергии по обобщенным скоростям

,

,

.

Возьмем производные по времени полученных выражений, имея в виду, что все обобщенные координаты и скорости являются функциями времени:

,

.

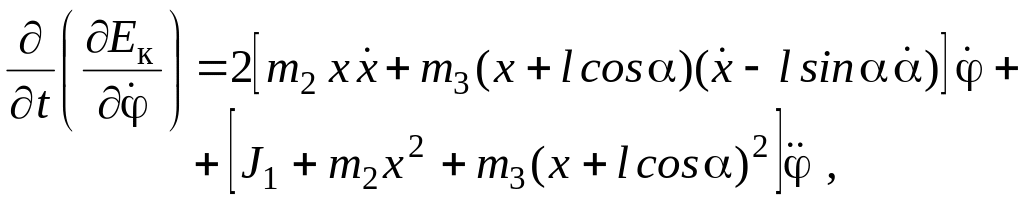
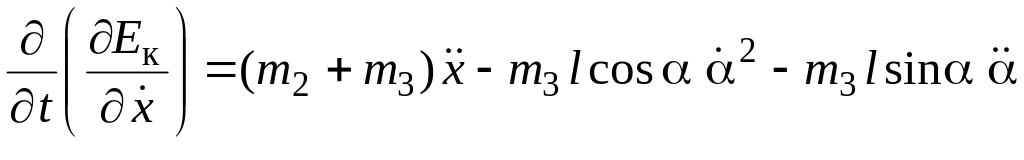6) Частные производные кинетической энергии по обобщенным координатам

,

,

.

7) В результате подстановки (4.7) и (4.14) в векторное уравнение Лагранжа (4.1) и последующих преобразований математическая модель стенда описывается системой трех обыкновенных дифференциальных уравнений:

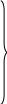
(4.15)

Уравнения в форме (4.15) обычно преобразуют к нормальной форме (4.2) Коши, разрешая их относительно обобщенных ускорений.

Как следует из (4.15), рассматриваемый механизм является нелинейным объектом третьего порядка с перекрестными связями по обобщенным координатам и скоростям.

Для решения уравнений динамики (4.15) целесообразно применение широко распространенных математических систем (Maple V R3…R6, Matlab 5.0…6.5, MathCAD Pro (Premium), Mathematica 2…4 и др.). Прежде всего, пакеты символьной математики этих математических систем позволяют преобразовать векторно-матричное описание (4.15) к нормальной форме Коши, исключив многочисленные рутинные преобразования. Кроме того, эти математические системы позволяют выполнить численное интегрирование систем линейных и нелинейных дифференциальных уравнений, наглядно представить результаты вычислений в виде таблиц и графиков и решить целый перечень задач математического моделирования динамических систем.