Синтез свободного движения сау

Управляемый свободный процесс в системе определяется парой матриц A, B объекта управления и матрицей регулятора состояния, призванной обеспечивать оптимальность переходных свободных движений при произвольных начальных значениях вектора состояния X(0). На первом этапе синтеза будем полагать равными нулю все внешние аддитивные воздействия . Тогда управление свободным движением примет вид

(10.20)

Для нахождения матрицы воспользуемся теоремой об n интервалах дискретного управления в сочетании с принципом оптимальности Беллмана [5]. Не снижая общности выкладок будем полагать, что оптимальное свободное движение системы завершается через n тактов дискретного управления в нулевой точке пространства состояний . Сформируем расширенный вектор-столбец состояния

V(t) = col [X(t), U(kT)] (10.21)

и перепишем уравнение для случая управляемого свободного движения в виде

(10.22)

где D – матрица управляемого состояния размерности (n+m)(n+m),

. (10.23)

Зададимся некоторой произвольной дискретной управляющей последовательностью U(kT), k = –1, –2, ... , –n и рассмотрим движение системы в обратном времени, т. е. примем конечное нулевое состояние системы за начальное. Проинтегрируем уравнение (10.22) при нулевых начальных условиях X(0) = 0, воспользовавшись аппаратом переходных матриц состояния, получим векторное дискретное уравнение состояния

(10.24)

где – расширенная обратная матрица перехода.

Сформируем матрицы дискретного управления W размерности и дискретного состояния G размерности в виде

W = [ U(-T) U(-2T) ... U(-nT) ] , (10.25)

G = [ X(-T) X(-2T) ... X(-nT) ] . (10.26)

Поскольку не наложены какие-либо ограничения на множества управляющих воздействий и дискретные состояния системы, а также, по определению, система находилась в нулевом начальном состоянии, очевидно, что ее движение в обратном (по отношению к принятому при синтезе) направлении будет носить оптимальный по быстродействию апериодический характер. Следовательно, с учетом выражения (10.20) искомую матрицу можно найти в виде

. (10.27)

Решение векторно-матричного уравнения (10.27) будет единственным при полном ранге матрицы G, т. е. если rank(G) = n.

Синтез вынужденного движения сау

На втором этапе синтеза определим матрицы , , входящие в выражение (10.19) для чего рассмотрим вынужденное движение системы.

Представим вектор-столбец установившихся состояний САУ в виде

(10.28)

где – подвектор размерности m1, определяющий заданное установившееся состояние системы, т. е. ,

– подвектор размерности (n-m)1, включающий в себя остальные координаты состояния системы управления.

Соответствующую матрицу установившихся состояний представим в виде блочной матрицы

(10.29)

где – подматрицы соответственно размерности .

Представим все аддитивные воздействия на систему в виде обобщенного вектора-столбца размерности (2m+d)1 задающих и возмущающих воздействий

(10.30)

и зададимся численными значениями его 2 компонент 2 раз, из которых сформируем неособую матрицу Q аддитивных воздействий размерностью (2m+d)(2m+d) в виде

. (10.31)

Тогда, с учетом введенных обозначений (10.19)… 10.30), уравнение 10.18) для квазиустановившихся состояний системы ( , ) можно переписать в виде

. (10.32)

Подставим векторы установившихся состояний в уравнение (10.19) и выразим искомую блочную матрицу

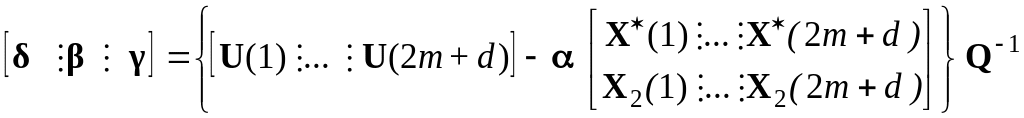(10.33) Матрицы , ,  определяются однозначно при полном ранге матрицы Q, что легко обеспечить соответствующим заданием значений аддитивных воздействий, либо формированием заведомо невырожденных матриц размерности (2m+d)(2m+d).

Таким образом, результирующее дискретное управление в форме (10.19) представляет собой цифровой регулятор состояния, обеспечивающий комбинированное апериодическое управление по отклонению выходной координаты от заданного значения и по возмущающим воздействиям, а также астатизм первого порядка по задающим воздействиям.

Рекомендуемая ЛИТЕРАТУРА

Основная литература:

1. Терехов В.М. Элементы автоматизированного электропривода. М.: Энергоатомиздат, 1987 – 224 с.

2. Башарин А.В., Новиков В.А., Соколовский Г.Г. Управление электроприводами: Учебное пособие для вузов. – Л.: Энергоиздат. Ленингр. Отд-ние, 1982. – 392 с.

Дополнительная литература:

3. Синтез электромеханических приводов с цифровым управлением / Вейц В.Л., Вербовой П.Ф., Вольберг О.Л., Съянов А.М.; Отв. Ред. Войтех А.А.; АН Украины. И-нт электродинамики. Киев: Наук. Думка, 1991. – 232 с.

4. Теория автоматического управления: Учеб. Для вузов / Брюханов В.Н., Косов М.Г., Протопопов С.П. и др. / ред. Соломенцев Ю.М. – М.: Высш. Шк., 2000. – 268 с.