10.3. Синтез цифровых систем управления

Существует множество методов синтеза цифровых систем управления,

основанных на описании управляемых динамических процессов, как в частотной области, так и во временной области [1-4].

Для синтеза цифровых САУ применяют, в частности:

• метод дискретизации по времени аналоговых регуляторов класса “вход/выход” (метод аналогий) или метод билинейного преобразования;

• метод переменного коэффициента усиления;

• методы аналитического конструирования дискретных регуляторов состояния САУ.

10.3.1. Метод дискретизации аналоговых регуляторов класса “вход - выход”

Данный метод основан на применении рассмотренных выше процедур

синтеза линейных аналоговых САУ. В качестве критериев оптимальности принимают общепринятые при синтезе таких систем интегральные квадратичные функционалы, а, следовательно, динамические процессы в оптимизированных контурах регулирования соответствуют реакциям тех или иных оптимальных фильтров, например фильтров Баттерворта n-го порядка. Синтезированное аналоговое устройство управления содержит, как правило, один или несколько последовательно включенных регуляторов (корректирующих устройств) класса “вход/выход”.

Суть метода заключается в замене передаточных функций синтезированных непрерывных регуляторов их дискретными аналогами. Отсюда и второе название данного метода синтеза – метод аналогий.

Для преобразования аналоговых передаточных функций регуляторов в дискретные применяют замену непрерывных операторов p Лапласа их дискретным аналогом z = f(p). В качестве примера рассмотрим дискретизацию непрерывного ПИД-закона регулирования. Процедура преобразования иллюстрируется рис. 10.4.

Входным воздействием регулятора является ошибка регулирования

(e(t) для непрерывного и e(kT) для дискретного), выходным – сигнал управления (u (t) для непрерывного и u (kT) для дискретного).

Приведенное преобразование основано на замене:

(10.14)

- при формировании интегральной составляющей ПИД–закона регулирования;

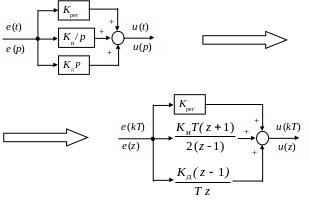
Рис. 10.4. Преобразование непрерывного ПИД- регулятора в его

дискретный аналог

(10.15)

- при формировании дифференциальной составляющей ПИД–закона регулирования.

Заметим, что с целью обеспечения точности отработки интеграла от ошибки регулирования при замене оператора p на z применена экстраполяция первого порядка (метод трапеций). Параметры К_рег, К_и, К_Д получены в результате синтеза аналогового ПИД- регулятора, Т – временной интервал между двумя соседними значениями управляющего воздействия (такт управления).

Применение этого метода синтеза предполагает, что дискретизацией аналоговых сигналов по уровню в силу достаточной длины разрядной сетки цифровых средств управления можно пренебречь, такт управления достаточно мал (как правило, на порядок меньше минимальной постоянной времени объекта управления). Также предполагатся, что периоды прерывания Т импульсного элемента датчиков обратной связи и регуляторов одинаковы и неизменны, причем синхронизированы во времени. Как показывают исследования [4] в цифровых электромеханических САУ такт прерывания не должен превышать 0,005 с. Обеспечение этих условий позволяет получить динамические характеристики цифровой САУ практически такие же, что и в непрерывной системе.