9.3.2. Система частотно-токового управления ад

Наибольшее распространение такие системы получили в станкостроении. Обычно СУ ЭП проектируют так, чтобы потосцепление ротора . Стабилизация потокосцепления необходима, чтобы, с одной стороны, недопустить насыщение магнитной системы, с другой, - недопустимое снижение магнитного потока и, соответственно, электромагнитного момента. В энергетическом отношении это наиболее выгодный режим работы АД.

На основании схемы замещения АД (см. рис. 4.8)

, (9.7)

где - абсолютное скольжение АД,

. (9.8)

Таким образом, потокосцепление и момент определяются током ротора и абсолютным скольжением. Связь между током ротора и током статора можно также найти из схемы замещения. Опуская промежуточные преобразования можно записать:

, (9.9)

где смысл функции понятен из рис. 9.9.

На практике нелинейную функцию обычно линеаризуют (см. пунктирную кривую на рис. 9.9). Тогда

. (9.10)

Р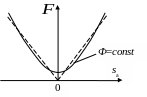 ис. 9.9. График функции

Таким образом, ток статора и электромагнитный момент АД зависят только от абсолютного скольжения, а следовательно их небходимо формировать именно в функции .

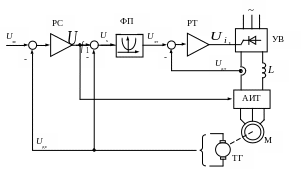Функциональная схема СУ ЭП приведена на рис. 9.10.

Рис. 9.10. Система частотно-токового управления АИТ

СУ ЭП является двухконтурной: внутренний контур - контур тока статора, внешний – контур скорости. Регулятор скорости формирует сигнал задания частоты тока статора, пропорциональный ошибке регулирования скорости. На вход функционального преобразователя ФП подается разность выходного сигнала регулятора скорости и сигнала датчика скорости U_дс, пропорционального скорости АД. Таким образом, на входе ФП формируется сигнал пропорциональный абсолютному скольжению

,

а, следовательно, выходной сигнал ФП сигнал может служить заданием тока статора или момента. На рис. 9.10 этот сигнал обозначен U_зт .

Раздельное управление током и частотой поля статора регуляторами тока и скорости обеспечивает простоту настройки СУ ЭП и высокое качество переходных процессов в электроприводе.

10. Дискретные и дискретно-непрерывные сау

10.1. Дискретизация сигналов и z-преобразование

В дискретных системах в отличие от непрерывных САУ имеется хотя бы одна координата состояния или управления, имеющая дискретный характер.

Достаточным условием дискретности систем управления является разрывная статическая характеристика.

Рис. 10.1. Функциональная схема дискретной САУ

Обозначения:

ДЭ – дискретный элемент;

НЧ – непрерывная часть;

- входной непрерывный сигнал;

- непрерывный сигнал ошибки;

- дискретный сигнал;

- непрерывный выходной сигнал.

Звено, в котором происходит дискретизация сигнала, называется дискретным элементом.

Дискретный характер имеют релейные, импульсные и цифровые сигналы.

Релейные САУ оперируют с сигналами, промодулированными по амплитуде. Например, релейное управление может быть реализовано с помощью двухпозиционного реле в соответствие с выражением

, (10.1)

где U_m – амплитуда управляющего воздействия,

- знаковая функция текущей ошибки управления,

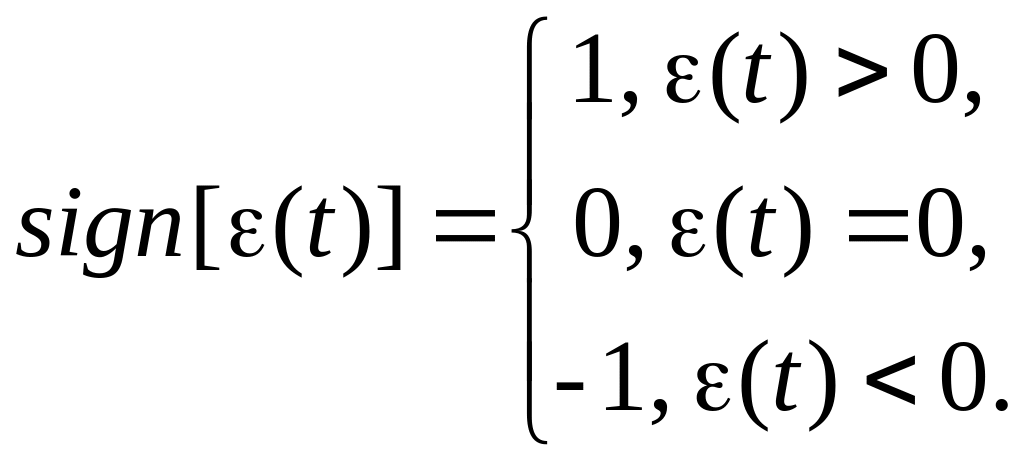(10.2)

В импульсных САУ имеются сигналы, промодулированные по времени (амплитудно-импульсные, широтно-импульсные, частотно-импульсные, фазо-импульсные и др.). Период T квантования сигналов в таких системах, как правило, постоянный. Например, широтно-импульсное нереверсивное управление можно представить в виде

, (10.3)

где - скважность управления как некоторая функция текущей ошибки управления, т. е. отношение времени t_у генерации управляющего воздействия с амплитудой U_m к периоду T управления, .

Цифровые системы управления оперируют с сигналами, представленными в виде цифровых кодов.

Непрерывные сигналы цифровой системы управления должны быть подвергнуты квантованию по времени и по уровню. Квантование непрерывного сигнала по времени реализуется с помощью импульсного модулятора, а квантование по амплитуде – с помощью амплитудного квантователя (рис. 10.2).

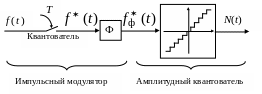
Рис. 10.2. Квантование непрерывных сигналов в цифровых САУ

В соответствие с теоремой Котельникова-Шеннона импульсный модулятор должен обеспечивать дискретизацию непрерывного сигнала по времени с частотой, по крайней мере, в 2 раза превышающей максимальную частоту изменения непрерывного сигнала. В любом случае частота квантования по времени должна быть выбрана такой, чтобы обеспечить наилучшее восстановление непрерывного сигнала (исходных данных) на интервале времени kT  t  (k+1)T по дискретным выборкам в k–е моменты времени, где k – номер такта квантования, T – период квантования.

Таким образом, процесс восстановления непрерывного сигнала может рассматриваться как процесс экстраполяции. Функция f(t) на интервале T может быть представлена в виде ряда Тейлора

, (10.4)

где - оценки производных в момент времени t = kT,

;

;

… .

Таким образом, для повышения точности экстраполяции сигнала требуется либо использовать информацию о выборках в прошедшие моменты времени, либо повышать частоту квантования по времени. Поскольку временное запаздывание оказывает неблагоприятное влияние на устойчивость систем управления с обратной связью, на практике обычно идут по второму пути, ограничиваясь удержанием лишь первого члена разложения ряда (10.4), т. е. принимают .

Импульсный модулятор, в котором удерживается лишь член f(kT), содержит 2 элемента (см. рис. 10.2) – квантователь непрерывного сигнала по времени с периодом T и фиксатор Ф нулевого порядка (экстраполятор нулевого порядка). Квантователь можно рассматривать как идеальный ключ, замыкающийся на бесконечно короткое время через каждые T секунд. Тогда выходной сигнал квантователя будет представлять собой решетчатую функцию

, (10.5)

где - значение входного непрерывного сигнала в момент времени kT замыкания ключа, k = 0… ,

- единичная импульсная функция ( -функция), генерируемая в момент времени k замыкания ключа.

Фиксатор сохраняет неизменным значение сигнала в течение периода T квантования. Передаточная функция фиксатора, реагирующего на импульсные воздействия вида (10.5), имеет вид

. (10.6)

Реакция импульсного модулятора (квантователя и фиксатора) на некоторое непрерывное воздействие f(t) приведена на рис. 10.3. Вертикальными стрелками обозначена реакция собственно квантователя, реализующего процесс дискретизации по времени.

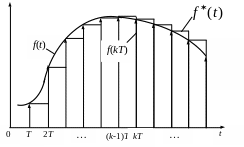
Рис. 10.3. Реакция импульсного модулятора на непрерывное

воздействие f(t)

В схемотехническом плане функции квантователя и экстраполятора (фиксатора) нулевого порядка реализуют с помощью устройства “выборки-хранения” (УВХ) [4].

Амплитудный квантователь обеспечивает квантование входного сигнала по уровню и выполняется на основе аналого-цифровых преобразователей (АЦП). При достаточно большом числе двоичных разрядов АЦП (12…24) квантованием по уровню при исследовании цифровых САУ обычно пренебрегают и цифровые САУ рассматривают как импульсные (амплитудно-импульсные с фиксатором нулевого порядка).

Анализ и синтез импульсных систем осуществляют с применением метода z-преобразования или метода пространства состояний.

Преобразование Лапласа квантованного по времени сигнала имеет вид

(10.7)

Сделаем замену , что позволит получить z-преобразование вида

(10.8)

где z - комплексная переменная, действительная и мнимая части которой определяются как

,

,

где

Анализ проекций комплексной переменной z на оси Re(z) и Im(z) позволяет сделать вывод, что область устойчивости дискретной САУ на комплексной плоскости ограничена окружностью единичного радиуса.

Физический смысл сомножителя при функции f (kT) - фиксация и запоминание в ячейках памяти ЭВМ ее текущего (k = 0) и предшествующих значений (k = 1, 2, …).