Динамическую точность систем стабилизации оценивают по величине

мгновенного максимального отклонения x_max или по величине среднеквадратичного отклонения x_сркв по отношению к заданному значению выходной координаты (%). Вторая оценка полнее характеризует точность системы, так как основана на статистических характеристиках САУ.

В идеальном случае динамическая погрешность отработки сигнала задания в САР должна быть равна нулю. На самом деле, ограничения, накладываемые на ресурсы управления, вынуждают искать некий компромисс, в частности - между временем регулирования и перерегулированием выходной координаты. При этом наиболее часто прибегают к одному из двух подходов.

6.2.1. Форсирование управляющего воздействия.

Этот способ позволяет очень эффективно снизить динамическую ошибку регулирования в простейших САР. В качестве примера рассмотрим процесс регулирования тока возбуждения генератора постоянного тока. На рис. 6.9. приведены функциональная схема (а) объекта управления и переходные процессы (б) напряжения и тока возбуждения без форсирования и с форсированием управляющего воздействия. Тиристорный возбудитель (ТВ) представлен безынерционным звеном, цепь тока возбуждения – апериодическим звеном 1-го порядка. Эквивалентная постоянная времени цепи возбуждения принята равной .

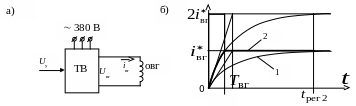
Рис. 6.9. К оценке эффективности форсирования управляющего

воздействия

Кривая 1 – реакция тока возбуждения на ступенчатое задающее воздействие без форсировки управляющего водействия, кривая 2 - реакция тока возуждения на то же самое задающее воздействие с двухкратной форсировкой управляющего воздействия. Форсировка осуществляется кратковременно на время t_рег1, при котором ток возбуждения достигает заданного значения. Заметим, что форсирование сигнала управления позволяет в несколько раз снизить время регулирования и существенно уменьшить динамическую ошибку регулирования, однако далеко не всегда осуществимо. В частности, в рассмотренном примере тиристорный возбудитель для реализации двукратной форсировки должен иметь соответствующий запас по напряжению, а, следовательно, запас по углу отпирания тиристоров. К недостаткам этого метода следует отнести необходимость применения нетиповых корректирующих звеньев (релейного элемента и компаратора).

6.2.2. Компенсация больших постоянных времени объекта управления

Выполняется после структурно-параметрической декомпозиции объекта управления. Допустим, в результате структурной декомпозиции выделен объект управления, структурная схема которого приведена на рис. 6.10.

Этот объект управления содержит 2 апериодических звена 1-го порядка с большими постоянными времени (БПВ) T₁ и T₂ и n звеньев с малыми постоянными времени (МПВ) ₁ … _n , причем _i << T₁, T₂, i = 1…n.

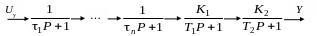
Рис. 6.10. Структурная схема объекта управления

Тогда, учитывая, что произведением МПВ можно пренебречь, запишем выражение для эквивалентной МПВ:

Эту постоянную времени часто называют некомпенсированной малой постоянной времени, поскольку, во-первых, компенсации подлежат только БПВ, во-вторых, любая технически реализуемая САУ после компенсации всех БПВ все равно будет обладать некоторой инерцией и именно эта некомпенсированная МПВ будет определять быстродействие системы.

Таким образом, параметрическая декомпозиция ОУ приводит к замене всех звеньев с МПВ одним эквивалентным звеном

Установим на входе ОУ компенсирующее (корректирующее) ПИД – звено

.

Тогда передаточная функция объекта управления со звеном компенсации (разомкнутого контура регулирования)

Как видим, ОУ существенно упростился и синтез оптимального управления им уже не представляет сложностей (см. раздел 7). В замкнутой СУ ЭП корректирующее звено целесообразно включить в структуру регулятора.

Заметим, что все сказанное справедливо лишь в случае идеальной компенсации БПВ объекта управления. В действительности параметры ОУ всегда рассчитываются (оцениваются) с некоторой погрешностью, при функционировании СУ ЭП претерпевают температурные, временные и прочие изменения. Параметры компенсирующего звена также могут подвергаться температурному, временному дрейфу. Все это приводит к недокомпенсации или перекомпенсации БПВ и, как следствие, к снижению эффекта от компенсации. Кроме того, компенсация довольно больших постоянных времени требует соответствующих затрат энергии, а реальные ограничения, накладываемые на энергетические ресурсы, приводят к сужению зоны малых отклонений координат ОУ, т. е. к нелинейности СУ ЭП. Тем не менее, данный метод улучшения динамических показателей широко применяется в сочетании с процедурами синтеза оптимальных систем управления.