6.2. Динамика су эп. Свободные и вынужденные переходные процессы

Динамические режимы СУ ЭП характеризуются переходными состояниями системы при изменении входных (задающих и (или) возмущающих) воздействий. При этом различают свободные и вынужденные переходные процессы.

Назовем процесс вынужденным, если промежуток времени между моментом t_з (t_в) приложения задающего (возмущающего) воздействия X(t) и моментом наблюдения выходной величины Y(t) равен бесконечности. В дальнейшем будем полагать моменты времени приложения воздействий равными нулю. Тогда процесс изменения выходной величины Y(t) в соответствие с теоремой свертывания (умножения изображений) будет иметь вид [3]

, (5.10) где -импульсная переходная функция по задающему (возмущающему) воздействию.

Свободный (собственный) процесс в системе определяется решением однородного дифференциального уравнения, описывающего САУ, протекает под действием ненулевых начальных условий Y(t₀) и в устойчивых системах асимптотически затухает:

, (5.11)

где – матрица перехода системы из начального состояния Y(t₀) в текущее состояние Y(t).

Полное решение уравнения движения линейных СУ ЭП представляет собой сумму решений уравнений свободного и вынужденного движений.

В качестве примера на рис. 5.3 приведена реакция электродвигателя постоянного тока (полное решение уравнения движения) на ступенчатое приложение номинальной нагрузки M_сн к его валу (возмущающего воздействия).

При приложении нагрузки скорость двигателя падает, причем имеет место колебательный процесс. Максимальный динамический провал скорости превышает статическое падение скорости (см. рис. 5.1).

Вынужденное движение соответствует новому установившемуся состоянию - номинальной скорости электродвигателя. Время переходного процесса (перехода в новое установившееся состояние) составляет t_рег .

Задача исследования динамических свойств СУ ЭП в концепции современной теории управления решается путем решения векторно-матричного уравнения состояния (4.29) относительно желаемой, как правило, выходной переменной СУ ЭП. Для этой цели применяют матрицу переходных состояний.

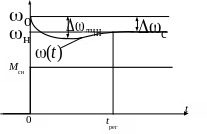
Рис. 5.3. Реакция электродвигателя постоянного тока на возмущающее воздействие в виде ступени номинальной нагрузки на валу

Если известно в момент времени t = 0 начальное состояние X(0) объекта управления и вектор управляющих воздействий U(0) (призванный оптимизировать движение системы), то уравнение движения системы во времени t (здесь и далее полагается, что возмущения F(t), действующие на систему, равны нулю) определяется выражением [2]:

. (5.12)

Первое слагаемое в векторно-матричном выражении (5.12) отражает свободное движение многомерной линейной САУ и аналогично скалярному выражению (5.11), описывающему свободное движение одномерной системы. Второе слагаемое в (5.12) отражает вынужденное движение многомерной линейной САУ и аналогично выражению (5.10), описывающему вынужденное движение одномерной системы.

Матрицу , определяющую динамические процессы в системе, называют переходной матрицей состояния или просто матрицей перехода. Существует ряд методов нахождения этой матрицы, базирующихся на описании САУ как во временной области (в форме дифференциальных или векторно-матричных уравнений), так и в области комплексного переменного p (в операторной форме или в форме структурных схем). Наиболее часто для определения матрицы перехода во временной области используют матричную экспоненциальную функцию в виде разложения ее в ряд с ограниченным числом k ( ) членов ряда [2]:

, (5.13)

где E – единичная матрица,

! – знак факториала.

Решение векторно-матричного уравнения (4.29), описывающего линейную систему управления, можно получить и в области комплексного переменного p, применив преобразование Лапласа:

, (5.14)

где – преобразование Лапласа переходной матрицы состояния,

т. е. .

В частности для свободного движения системы под действием ненулевого начального состояния X(0) можно записать

. (5.15)

На практике для нахождения переходной матрицы состояния многомерных САУ применяют системы программирования, упомянутые в главе 4. Они базируются на численных методах решения уравнения (5.13) для заданного времени t = T перехода системы из некоторого начального состояния в последующее, отстоящее на время T, состояние.

В качестве примера рассмотрим нахождение матрицы перехода для рассматриваемого ранее объекта управления – электродвигателя постоянного тока, регулируемого по цепи якоря.

Пусть векторно-матричная модель объекта управления задана уравнениями (4.29), (4.30), (4.31), причем зададимся U = U_я = 10 В, F = M_с = 0.

Зададимся также численными значениями параметров электродвигателя: R_э=1 Ом; T_э=0, 02 Гн; K_д=0,5 (Вс) , J_д = 1 .

В соответствие с (5.31) получим

; . (5.16)

Воспользуемся численным методом определения матрицы перехода, определяемой выражением (5.13) с числом членов разложения ряда, равным 20 (это очень высокая, может быть и неоправданная, точность вычисления матрицы перехода, позволяющая получить своего рода эталонное решение уравнений динамики системы).

Для расчета переходной матрицы состояния воспользуемся численной процедурой вычисления ряда (5.13) [4], причем зададимся приращением времени (T = 0,01 с) перехода из начального состояния в следующее состояние системы. В частности, в системе MatLab для расчета переходной матрицы состояния используется функция EXPM(A). Тогда получим

. (5.17)

Задаваясь некоторым ненулевым начальным состоянием объекта управления в момент времени t = 0, например i_я(0) = 0 (А), (рад/с), т.е. , получим численные значения вектора состояния в момент времени t = 0,01 с:

.

Умножая полученный вектор состояния на переходную матрицу состояния можно получить вектор состояния в момент времени 0,02 с и т. д. Результатом операции по применению матрицы переходных состояний на интервале времени перехода системы в новое установившееся состояние является переходный процесс, отражающий свободное движение системы. На рис. 5.4 приведена таблица расчета переходного процесса на первых 7-ми тактах расчета, а также кривые переходного процесса (в % от экстремальных значений координат электродвигателя).

Как видим, свободное движение системы из заданного начального состояния представляет собой “свободный выбег” электродвигателя за время, соответствующее переходу вектора состояния системы в нулевое установившееся состояние.

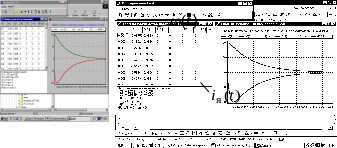
Рис. 5.4. Таблица расчета и графики свободного

движения электродвигателя

Аналогичным образом определяется движение системы под действием ненулевого управляющего воздействия U_я, т. е. вынужденное движение системы. Пусть при нулевом векторе начального состояния системы на якорную обмотку подали напряжение U_я = 10 В. Для расчета реакции электродвигателя воспользуемся численным методом решения векторно-матричного уравнения (5.12). Такт расчета примем равным приращению времени перехода системы из одного состояния в следующее, задаваемого матрицей перехода, т. е. . На рис. 5.5 приведена таблица расчета реакции системы на первых 7-ми тактах расчета, а также кривые вынужденного переходного процесса (в % от экстремальных значений координат электродвигателя). Установившееся значение скорости электродвигателя (в данном случае оно является экстремальным) равно 5 (рад/с), установившееся значение тока якоря равно нулю.

Суммирование реакций САУ в соответствие с (5.12) дает результирующую реакцию системы (рис. 5.6).

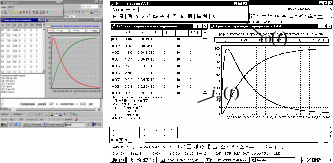
Рис. 5.5. Таблица расчета и графики вынужденного

движения электродвигателя

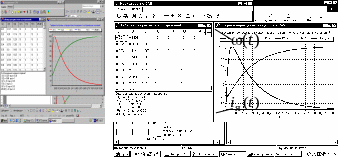
Рис. 5.6. Таблица расчета и графики полного переходного

процесса в электродвигателе

Сразу отметим, что эта реакция системы, скорее всего, будет неудовлетворительной с точки зрения обеспечения требуемого качества управления, что объясняется произволом выбора приращения управляющего воздействия (управляющее воздействие нами выбрано постоянным и равным 10В на протяжении всего времени переходного процесса). Определение оптимального изменения во времени управляющего воздействия – задача структурно-параметрического синтеза системы управления. Этот вопрос рассматривается в гл. 10.