
- •Министерство образования России
- •Используемая аббревиатура
- •Введение
- •1. Классификация систем управления электроприводами
- •1. По степени автоматизации функций управления:
- •2. По характеру протекания процессов в су эп и, соответственно, форме математического описания:
- •3. По наличию существенных нелинейностей в су эп:
- •По типу обратных связей:
- •По принципу управления (характеру задач управления):
- •По числу и связности каналов управления:
- •По способу преобразования подводимой энергии:
- •По типу регулируемой локальной координаты:
- •По типу регуляторов, применяемых в устройстве управления:
- •По типу элементной базы устройства управления:
- •2. Обобщенная функциональная схема су эп
- •3. Основные задачи исследования и этапы проектирования
- •3.1. Основные задачи исследования су эп
- •3.2. Основные положения системного подхода при проектировании су эп
- •3.3. Стадии проектирования, регламентированные госТом
- •4. Математические модели элементов су эп
- •4.1. Методы описания и исследования динамических управляемых объектов в частотной и временной области
- •4.2. Уравнение Лагранжа и дифференциальные уравнения электромеханических систем управления (эмсу)
- •4.3. Линеаризация элементов су эп
- •4.4. Двигатель постоянного тока как объект управления
- •4.5. Асинхронный двигатель как объект управления
- •4.6. Электромашинный преобразователь как объект управления
- •4.7. Тиристорные преобразователи как объекты управления
- •4.8. Математические модели датчиков координат су эп
- •4.9. Математические модели регуляторов су эп
- •5. Статические и динамические характеристики су эп
- •5.1. Статика су эп. Коэффициенты ошибок су эп по положению, скорости и ускорению
- •6.2. Динамика су эп. Свободные и вынужденные переходные процессы
- •Общие принципы построения су эп
- •6.1. Релейно-контакторные су эп. Реализация пуско-тормозных режимов су эп постоянного и переменного тока
- •6.1.1. Рксу асинхронным двигателем с короткозамкнутым ротором
- •6.1.2. Рксу асинхронным двигателем с фазным ротором
- •6.1.3. Рксу двигателем постоянного тока
- •6.2. Системы стабилизации выходной координаты объекта управления. Типовые методы улучшения динамики су эп
- •В статике, т. Е. В установившихся (квазиустановившихся) режимах функционирования систем стабилизации можно сформулировать два основных тесно взаимосвязанных требования:
- •Динамическую точность систем стабилизации оценивают по величине
- •6.2.1. Форсирование управляющего воздействия.
- •6.2.2. Компенсация больших постоянных времени объекта управления
- •6.3. Системы программного управления. Способы ограничения координат су эп
- •6.3.1. Ограничение координат сау применением дополнительных нелинейных обратных связей.
- •6.3.3. Ограничение координат сау посредством ограничения задающих воздействий. Этот способ ограничения координат нашел широкое распространение в
- •6.4. Следящие системы управления и системы воспроизведения движений. Понятие добротности су эп
- •7. Методы синтеза су эп
- •7.1. Общая постановка задачи синтеза
- •7.2. Типовые регуляторы и корректирующие звенья су эп
- •7.3. Последовательная коррекция су э п частотными методами
- •7.3.1. Коррекция с опережением по фазе
- •7.3.2. Коррекция с отставанием по фазе
- •7.3.3. Коррекция введением интеграторов
- •7.4. Синтез систем с подчиненным регулированием координат
- •7.5. Методика структурно-параметрического синтеза контуров регулирования су эп по желаемой передаточной функции
- •7.6. Синтез оптимальных по быстродействию су эп с апериодической реакцией
- •8. Су эп постоянного тока
- •8.1. Синтез системы регулирования скорости “Тиристорный преобразователь - двигатель постоянного тока”
- •8.1.1. Синтез контура регулирования тока якоря
- •8.1.2. Синтез контура регулирования скорости.
- •Интегрирующей сар скорости при ударном приложении нагрузки на валу электропривода
- •8.2. Синтез системы регулирования скорости “Генератор - двигатель постоянного тока”
- •8.2.1. Одноконтурная сар тока якоря
- •8.2.2. Двухконтурная сар тока якоря
- •8.3. Синтез системы регулирования э.Д.С. Двигателя
- •Для расчета параметров принципиальной схемы пи-регулятора э.Д.С.
- •8.4. Система двухзонного регулирования скорости Применяется в тех случаях, когда требуется обеспечить работу
- •8.5. Системы регулирования положения рабочего органа
- •8.5.1. Сар положения с линейным регулятором
- •Подставляя в это соотношение выражение для Kрп в режиме средних перемещений получим
- •8.6. Следящие системы управления электроприводами
- •8.6.1. Добротность сау, синтез инвариантных сау по отношению к задающим и возмущающим воздействиям
- •8.6.2. Типовые структуры следящих электроприводов
- •9. Су эп переменного тока
- •9.1. Способы управления асинхронным двигателем
- •9.2. Силовые преобразователи, применяемые для управления асинхронными электродвигателями
- •9.2.1. Преобразователи частоты с автономным инвертором напряжения
- •9.2.2. Преобразователи частоты с автономным инвертором тока
- •9.2.3. Преобразователи частоты с непосредственной связью с сетью
- •9.3. Су эп со звеном постоянного тока
- •9.3.1. Система частотного управления ад с iR- компенсацией
- •9.3.2. Система частотно-токового управления ад
- •10. Дискретные и дискретно-непрерывные сау
- •10.1. Дискретизация сигналов и z-преобразование
- •10.2. Дискретные передаточные функции и разностные уравнения
- •10.3. Синтез цифровых систем управления
- •10.3.1. Метод дискретизации аналоговых регуляторов класса “вход - выход”
- •10.3.2. Метод переменного коэффициента усиления
- •10.3.3. Метод синтеза апериодических дискретно-непрерывных сау с регуляторами состояния
- •Синтез свободного движения сау
- •Синтез вынужденного движения сау
4.8. Математические модели датчиков координат су эп
Основными координатами электромеханических САУ являются: скорость вращения или линейная скорость Vлин перемещения рабочего органа, угловое положение вала или линейное перемещение S рабочего органа, статическая нагрузка на валу рабочего органа Мс, напряжение на активной или активно-индуктивной нагрузке Uн, натяжение н нити или полотна, усилие рабочего органа, температура объекта управления, давление жидкостей или газов и т. д. ММ датчиков этих координат САУ обычно представляются в виде безынерционных звеньев: Кдс , Кдп , Кдм ... . Иногда, в частности при необходимости фильтрации, сглаживания пульсаций измеряемых сигналов, ММ датчиков координат САУ представляют в виде инерционных моделей 1-го или более высокого порядка. Тот же тахогенератор постоянного тока обладает: оборотными пульсациями вследствие неравномерности магнитного зазора, коллекторными пульсациями, зубцовыми и полюсными пульсациями. В силу этого при синтезе САР скорости тахогенератор, как правило, рассматривают в виде апериодическое звено 1-го порядка. Величина постоянных времени фильтров на выходе датчиков координат обычно не превышает 5 мс.
Полоса пропускания современных устройств преобразования, приема/передачи информации о координатах состояния промышленных электромеханических САУ достаточно высока по сравнению с полосой пропускания силовых модулей, чтобы их ММ можно было рассматривать безынерционными звеньями.
4.9. Математические модели регуляторов су эп
Устройство управления (УУ) состоит из регуляторов, следовательно, для проектирования и исследования СУ ЭП необходимо иметь формальные модели этих регуляторов. В качестве регуляторов систем автоматизации и управления применяются электронные регуляторы на основе аналоговой и цифровой элементной базы, механические, пневматические, гидравлические, электропневматические регуляторы с той или иной характеристикой и т.п.
Независимо от технологического назначения регуляторов (регуляторов скорости, положения рабочего органа, давления, натяжения, температуры и т. д.) все они подразделяются на 2 больших класса:
- параметрические регуляторы класса «вход/выход» (П- , ПИ-, ПИД- и т. п. регуляторы );
- регуляторы состояния САУ (апериодические, модальные и т.п.). В отличие от регуляторов 1-го класса они контролируют все состояние системы либо ее некоторой части, т. е. имеют обратные связи по полному либо усеченному вектору состояния системы.
Первый класс регуляторов на функциональных схемах СУ ЭП обозначается в виде переходной функции, которую имеет данный регулятор, например в виде, приведенном на рис. 4.17а.

Обозначения на схеме:
Хвх - входной сигнал - сигнал ошибки регулирования той или иной координаты САУ;
Увых- выходной сигнал регулятора.
Регуляторы состояния (рис. 4.17б), в отличие от регуляторов класса «вход/выход» имеют как минимум обратную связь по вектору состояния. В общем случае они еще имеют входные задающие и возмущающие воздействия.
Обозначения на схеме:
Xз - вектор задающих воздействий;
Xз=хз1 хз2 хз3 ... хзk T;
X - вектор (полный или усеченный) состояния САУ;
X=х1 х2 х3 ... хn T;
Yвых - вектор выходных воздействий регулятора;
Увых=у1 у2 у3 ... уmT;
F - вектор возмущающих воздействий;
F ==f1 f2 f3 ... fd T.
При k = m = 1 векторный регулятор состояния преобразуется в скалярный регулятор.
Рассмотрим наиболее часто применяемые в различных САУ параметрически оптимизируемые регуляторы класса «вход/выход».
Их можно представить в виде усилительного звена - операционного усилителя (рис 4.18).
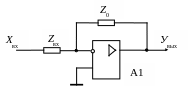
Рис.
4.18. Функциональная схема регулятора
класса «вход/выход»
Обозначения на схеме:
A1 - операционный усилитель;
Zвх, Z0 - комплексные сопротивления во входной цепи и в цепи обратной связи операционного усилителя.
Математическую модель таких регуляторов чаще всего представляют либо в виде передаточной функции (структурной схемы), либо в виде дифференциальных уравнений (переходной функции). Входной сигнал представляет собой разность между задающим сигналом и сигналом обратной связи по регулируемой координате (ошибку регулирования). Обратная связь всегда отрицательна, а значит либо входной, либо выходной сигнал операционного усилителя должен быть инверсным. На рис. 4.19. приведена принципиальная электрическая схема простейшего регулятора класса «Вход/Выход» с пропорциональнй структурой.
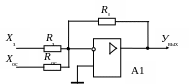
Рис.
4.19. Принципиальная электрическая схема
регулятора класса
«вход/выход»
Обозначения на схеме:
A1 - операционный усилитель;
Rз, R0, Rос - активные сопротивления соответственно в цепи задания, собственной обратной связи операционного усилителя и обратной связи регулятора;
Хз - сигнал задания;
Хос - сигнал обратной связи с датчика регулируемой координаты;
Yвых - выходной сигнал регулятора.
П ри
математическом описании регуляторов
применим
следующую последовательность:
принципиальная схема регулятора
передаточная функция временная
характеристика (реакция на единичное
ступенчатое воздействие), т.е. переходная
характеристика переходный процесс
ри
математическом описании регуляторов
применим
следующую последовательность:
принципиальная схема регулятора
передаточная функция временная
характеристика (реакция на единичное
ступенчатое воздействие), т.е. переходная
характеристика переходный процесс
и зображение блок-схемы регулятора (функциональная схема).
1. Пропорциональный регулятор (П-регулятор).
Принципиальная схема регулятора приведена на рис. 4.19. Будем полагать, что на входе регулятора - сигнал ошибки регулирования Хвх , причем Хвх = Хз - Хос. При этом вместо двух резисторов RЗ и Rос используется один - Rвх .
Передаточная функция регулятора
![]() (4.49)
(4.49)
Хотя пропорциональный регулятор теоретически позволяет пропускать через себя сигналы всего спектра частот, в действительности его частотные свойства носят ограниченный характер, поскольку в области высоких частот коэффициент передачи Крег будет снижаться и появится фазовый сдвиг между Хвх к Увых .. Ограничение спектра пропускания частот осуществляется цепями внутренней коррекции операционных усилителей и реальная полоса пропускания пропорциональных регуляторов ограничивается сотнями Гц или единицами кГц. Цепи коррекции операционных усилителей позволяют повысить помехозащищенность канала регулирования.
Временная характеристика регулятора:
Увых(t)=КрегХвх(t).
П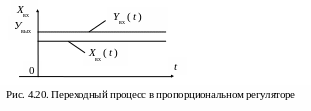 ереходный
процесс в регуляторе будет иметь вид,
изображенный на рис. 4.20.
ереходный
процесс в регуляторе будет иметь вид,
изображенный на рис. 4.20.
Функциональная схема пропорционального регулятора приведена на рис. 4.21.
 2.
Интегральный регулятор (И-регулятор).
2.
Интегральный регулятор (И-регулятор).
 Принципиальная
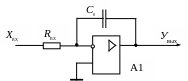
схема регулятора приведена на рис. 4.22.
Принципиальная
схема регулятора приведена на рис. 4.22.
Рис. 4.22. Принципиальная электрическая схема интегрального регулятора
Передаточная функция регулятора
![]() (4.50)
(4.50)
где TИ - постоянная времени интегратора, TИ = RВХС0 .
Временная характеристика регулятора:
Увых(t)= Увых(0)+1/( RВХС0)Хвх(t)t.
П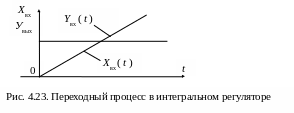 ереходный
процесс в регуляторе при нулевых
начальных условиях (Увых(0)=0)
будет иметь вид, изображенный на рис.
4.23.
ереходный
процесс в регуляторе при нулевых
начальных условиях (Увых(0)=0)
будет иметь вид, изображенный на рис.
4.23.
Функциональная схема интегрального регулятора приведена на рис. 4.24.
 3.
Дифференциальный регулятор (Д-регулятор).
3.
Дифференциальный регулятор (Д-регулятор).
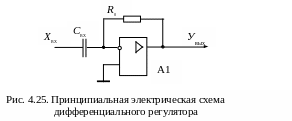 Принципиальная
схема регулятора приведена на рис. 4.25.
Принципиальная
схема регулятора приведена на рис. 4.25.
Передаточная функция регулятора
![]() (4.51)
(4.51)
где TД - постоянная времени интегратора, TД = R0СВХ.
Временная характеристика регулятора:
Увых(t)=TД(t),
где (t) - дельта-функция Дирака.
Переходный процесс в регуляторе будет иметь вид, изображенный на рис. 4.26.
С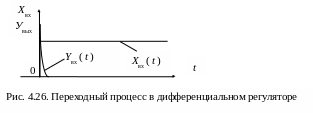 ледует
отметить, что ограниченная полоса
пропускания частот самих операционных
усилителей не позволяет реализовать
чистое (идеальное) дифференцирование.
Кроме того, в силу низкой помехозащищенности
дифференциальных регуляторов сложилась
практика применения реальных
дифференцирующих звеньев и принципиальные
схемы таких регуляторов несколько
отличаются от приведенной на рис. 4. 25.
ледует
отметить, что ограниченная полоса
пропускания частот самих операционных
усилителей не позволяет реализовать
чистое (идеальное) дифференцирование.
Кроме того, в силу низкой помехозащищенности
дифференциальных регуляторов сложилась
практика применения реальных
дифференцирующих звеньев и принципиальные
схемы таких регуляторов несколько
отличаются от приведенной на рис. 4. 25.
Функциональная схема дифференциального регулятора приведена на рис. 4.27.

4. Пропорционально-интегральный регулятор (ПИ-регулятор).
 Принципиальная
схема регулятора приведена на рис. 4.28.
Принципиальная
схема регулятора приведена на рис. 4.28.
Передаточная функция регулятора
![]() (4.52)
(4.52)
где KРЕГ - коэффициент передачи регулятора, KРЕГ = R0/RВХ;
TИ - постоянная времени интегратора, TИ = RВХС0 .
Временная характеристика регулятора:
Увых(t)= Увых(0) + ( KРЕГ + t/( RВХС0))Хвх(t).
Переходный процесс в регуляторе при нулевых начальных условиях будет иметь вид, изображенный на рис. 4.29.
Ф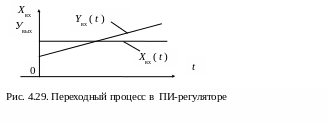
 ункциональная
схема пропорционально-интегрального
регулятора приведена на рис. 4.30.
ункциональная
схема пропорционально-интегрального
регулятора приведена на рис. 4.30.
Передаточную функцию пропорционально-интегрального регулятора часто представляют не в виде суммы двух слагаемых, а в виде так называемого изодромного звена
![]() , (4.53)
, (4.53)
где TИЗ - постоянная времени изодромного звена, TИЗ = R0C0 ,
TИ - постоянная времени интегрирования регулятора, TИ = RВХC0 .
ПИ-регулятор, включенный в структуру САУ, обеспечивает компенсацию одной большой постоянной времени объекта управления (см. раздел 8.1).
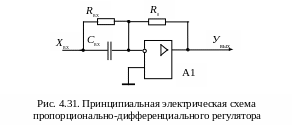
Пропорционально-дифференциальный регулятор (ПД-регулятор) Принципиальная схема регулятора приведена на рис. 4.31.
Передаточная функция регулятора
![]() (4.54)
(4.54)
где KРЕГ - коэффициент передачи регулятора, KРЕГ = R0/RВХ;
TД - постоянная времени интегратора, TД = R0СВХ.
Временная характеристика регулятора:
Увых(t)= KРЕГ Xвх(t) + TД(t),
где (t) - дельта-функция Дирака.
П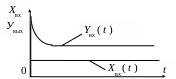 ереходный
процесс в ПД- регуляторе будет иметь
вид, изображенный на рис. 4.32, функциональная
схема регулятора приведена на рис. 4.33.
ереходный
процесс в ПД- регуляторе будет иметь
вид, изображенный на рис. 4.32, функциональная
схема регулятора приведена на рис. 4.33.
Рис. 4.32. Переходный процесс в ПД- регуляторе

6. Пропорционально-интегрально-дифференциальный регулятор (ПИД-
регулятор)
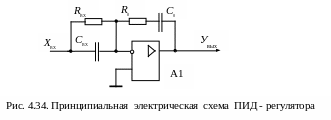 Принципиальная
схема регулятора приведена на рис. 4.34.
Принципиальная
схема регулятора приведена на рис. 4.34.
Передаточная функция регулятора
 (4.55)
(4.55)
где KРЕГ - коэффициент передачи регулятора, KРЕГ = R0/RВХ + CВХ/С0;
TИ - постоянная времени интегрирования, TИ = RВХС0;
TД - постоянная времени дифференцирования, TД = R0СВХ.
Временная характеристика регулятора:
Увых(t)= Увых(0) + KРЕГ Xвх(t) + (1/TИP) Xвх(t) + TД(t),
где (t) - дельта-функция Дирака.
Переходный процесс в регуляторе будет иметь вид, изображенный на рис. 4.35, функциональная схема приведена на рис. 4.36.
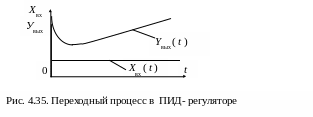

По аналогии с ПИ-регулятором ММ ПИД-регулятора часто представляют в виде изодромного звена второго порядка
![]() , (4.56)
, (4.56)
где ТИЗ,1 , ТИЗ,2 - постоянные времени изодромного звена; ТИЗ,1 = R0С0 , ТИЗ,2 = =RвхСвх .
ПИД-регулятор обеспечивает компенсацию двух больших постоянных времени объекта управления, обеспечивая интенсивность динамических процессов в САУ.
На практике часто применяются иные схемы ПД- и ПИД- регуляторов, обеспечивающие реальное дифференцирование ошибки регулирования и, соответственно, более высокую помехозащищенность САУ.
Помимо рассмотренных регуляторов применяются также регуляторы класса "вход/выход" иных структур: И-ПИ, И2-ПИ и т.п.
