1.6. Исследование процесса разрушения зерна в трубопроводе

В данном разделе работы производится оценка прочностных характерис­тик зерновки, движущейся в самотечном канале.

Предполагается, что силовое воздействие потока зерна и стенок канала на отдельную зерновку задано или может быть рассчитано, а оценка прочности зер­новки как композиционного тела проводится с пози­ций развития в ней трещин в результате действия на нее силовых факторов.

Если в качестве объекта исследования рассматри­вать зерновку типа пшеницы, то возможны 4 пре­дельных положения ее на поверхности самотечного трубопровода (рис. 1.6.1) или какое-либо из промежу­точных.

Причем для анализа силового воздействия потока зерносмеси на частицу зерна на поверхности трубо­провода, например в положении I, будем моделиро­вать ее двухопертой балкой (рис. 1.6.2), подверженной действию гидродинамического давления, и реакций в опорах.

При этом согласно предложенной гидродинами­ческой схеме расчета напряженного состояния в по­токе зерносмеси на балку действуют: силы давления р_х, р_у и касательное напряжение _ху, и, кроме того, реакции в точках А, В, а также сила трения зерновки о поверхность трубопровода как составляющей Х_А реакции опоры в точке А.

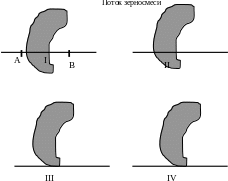
Рис. 1.6.1. Схема примерных предельных положений зерновки на поверхности самотечного трубопровода

Рис. 1.6.2. Схема силового воздействия потока зерносмеси на частицу зерна на поверхности трубопровода

В дальнейшем предполагается, что моделирующее зерновку тело является составным и упругим, состо­ящим из сплошной упругой среды некоторого услов­ного материала (например, оболочка+эндосперм) и включения другого (зародыша). Причем исходим из простейшей модели композита, когда тело вне выде­ленного включения считается однородным и изо­тропным с соответствующими эффективными упру­гими константами (правило смесей) [24]. Кроме того, для упрощения количественного анализа процесса разрушения зерновка рассматривается в виде безгра­ничного тела, а включение моделируется в виде эл­липтического цилиндра.

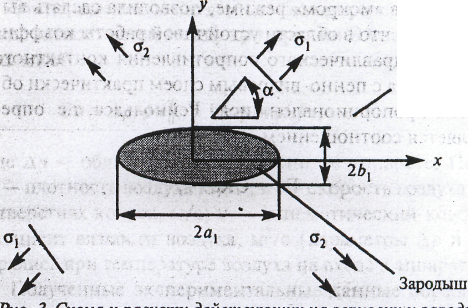
Рис. 1.6.3. Схема к расчёту действующих на зерновку и зародыш внешних усилий

Предполагая, что по своей форме зерновка при­ближается к эллипсоиду вращения (зерновки пше­ницы, ячменя и др.) с полуосями а₁, b₁ и площадью наибольшего миделевого сечения s₁ = а₁b₁, в каче­стве граничных условий по напряжениям на поверх­ности зерновки (т.е. вдали от зародыша) принима­ется (рис. 1.6.3):

_у^ = _у = Р₀, _ху^ = _ху = Т₀, (1.6.1)

где Р₀ = р(у = 0)/s₁ - нормальное давление; Т₀ = (у = 0)/s₁ — касательное напряжение на поверхности зерновки.

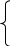
В свою очередь, если отношение модулей сдвига эндосперма и зародыша ₁/₂ < 1, и, кроме того, ве­личина 1 - (а₁ - b₁)/(а₁ + b₁) = < 1, то в предположении, что поле напряжений внутри включения однородно, формулы расчета касательного и нормального напряжений имеют вид [24]

_ху⁰ = _ху^/_, _у⁰ + _х⁰ = 4_у^_;

_у⁰ - _х⁰ = 2_у^(k₁ - 1)/_, (1.6.2)

где  = ₁(k₂ + 1), _ = ₁(k₂ + 1) + 2₂(k₁ - 1)(k₂ + 1), k_i = 3 - 4_i, _i -коэффициенты Пуассона (i = 1,2).

При анализе условий развития трещины в зернов­ке исходят из того, что в ней наиболее вероятно раз­витие трещин поперечного сдвига (так называемых трещин второго рода, рис. 1.6.4). Причем предполагает­ся, что берега трещины взаимодействуют по закону сухого (кулонова) трения.

Рис. 1.6.4. Схема перемещений поверхности трещины для основ­ных видов деформаций: а - нормальный отрыв; б - попереч­ный сдвиг; в - продольный сдвиг

Считается, что равновесное состояние трещины имеет место, когда касательное напряжение _ху компенсируется кулоновым трением F_тр и так называемым сцеплением материала F_сц = k₀. При этом силу трения вычисляют по формуле F_тр = f_тр_у, где f_тр = tg - коэффициент трения;  — угол внутреннего трения. Иначе говоря, должно иметь место соотно­шение _ху⁰ = k₀ - _у⁰tg. Поскольку сцепление матери­ала препятствует до некоторой величины растягива­ющим и сдвиговым напряжениям, то качественно

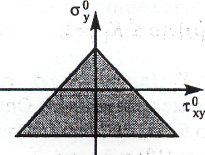
Рис. 1.6.5. Схема, включающая область допустимых значениё растягивающих и сдвиговых напряжений на краях трещины

область допустимых значе­ний ⁰, _у⁰ имеет вид, представленый на рис. 1.6.5. В та­ком случае коэффициент интенсивности напряже­ний K_II для трещины вы­бранного типа принима­ется пропорциональным величине:

F = _ху⁰ - k₀ + _у⁰tg (1.6.3)

Причем, так как согласно (1.6.2)

_у⁰ = _у^(2 + k₁ - 1)/_ = _у⁰(k₁ + 1)/_,

то вместо (1.6.3) получают:

F = - k₀ + _ху⁰/_ + _у^(k₁ + 1)tg/_. (1.6.4)

В свою очередь, как известно, напряжения _х, _у, _ху связаны с главными напряжениями ₁, ₂ зависи­мостями [25]:

_х, = [₁ + ₂ + (₁ - ₂)cos2]/2, _ху = (₁ - ₂)sin2/2;

(1.6.5)

_у = [₁ + ₂ - (₁ - ₂)cos2]/2 = ₂ + (₁ - ₂)sin²,

где  - угол наклона нормали к элементарной пло­щадке с осью x. В таком случае в силу (1.6.4), (1.6.5) находят:

F = - k₀ + (₁ - ₂)sincos/_ +

+ (k₁ + 1)[₂ + (₁ - ₂)sin²]tg/_ =

= - k₀ + C₂₂ + (₁ - ₂)(C₁sincos + C₂sin²); (1.6.6)

C₁ = /_ > 0, C₂ = (k₁ + 1)tg/_ > 0.

По поведению функции F на плоскости главных нормальных напряжений ₁, ₂ определяют область F(₁, ₂, )  0, граница которой отвечает условию разрушения включения (зародыша). А именно со­гласно (1.6.3) должно быть:

_ху⁰  k₀ - _у⁰tg. (1.6.7)

С целью найти экстремум функции F отыскивают производную (1.6.6) по :

dF/d = (₁ - ₂)(C₁cos2 + C₂sin2).

Откуда, приравнивая dF/d нулю, с учетом то­го, что ₁  ₂, имеют

tg2_ = C₁/ C₂, (1.6.8)

где _ — угол, при котором F достигает экстремаль­ное значение.

Дифференцируя (1.6.8) повторно по , получают

dF²/d_² = 2(₁ - ₂)(-C₁sin2_ + C₂cos2_),

или, если ₁ > ₂, то в силу (1.6.8)

dF²/d_² = 2(₁ - ₂)cos2_ < 0,

т.е. имеют максимум для F. Подставляя рассчитанное по (1.6.8) значение _ в (1.6.6), находят:

maxF(₁, ₂, ) = -k₀ + B₁₁ + B₂₂, (1.6.9)

где

B₁ = C₁sincos + C₂sin² = 0.5[C₁sin2 + С₂(1- cos2)] =

= 0.5[C₂ - (C₁² + C₂²)^1/2] < 0,

В₂ = C₂ - C₁sincos - C₂sin² = 0.5[C₂ + (C₁² + C₂²)^1/2] > 0.

В соответствии с найденными значениями угла _, коэффициентов В₁, В₂, а также симметрией ее отно­сительно биссектрисы ₁ = ₂ область допустимых значений главных напряжений на берегах трещины, называемая диаграммой разрушения включения [24] (зародыша), ограничена двумя наклоненными к оси х под острым углом прямыми ₁ = ₂ и прямой:

B₁₁ + B₂₂ = k₀. (1.6.10)

В дальнейшем, имея в виду, что исследуемая про­блема трещинообразования зависит от большого числа параметров, целесообразно перейти к безразмерным переменным. С этой целью преобразуют уравнение (1.6.10) к виду

(1.6.11)

где - безразмерные зна­чения главных напряжений, а коэффициенты С₁, С₂ - к форме

С₁ =

С₂ =

где  = ₂/₁,  - безразмерный параметр. Если обозначить

(1.6.12)

и опустить для простоты чёрточки, то вместо (11) по­лучим:

B₁₁ + B₂₂ = 1, С₁ = 1/(1 + ), С₂ = tg/(1 + ). (1.6.13)

И в результате

tg2 = - С₁/ С₂ = - сtg(1 + )/(1 + ).

Количественное моделирование на основе уравнения (1.6.13) проводили с помощью системы «Маtсhаd» для близ­ких к реальным в процессах трещинообразования зна­чениям безразмер­ных параметров  = 0.5 и  = 0.3 (рис. 1.6.6). Поскольку главные напряжения ₁ и ₂ равноправны, то построенные для различных значений коэффициен­тов трения прямые линии следует зер­кально отобразить относительно пря­мой ₁ = ₂ (рис. 1.6.7).

Рис. 1.6.6. Границы области допустимых значений главных напряжений на берегах трещины (1 – линия ₁ = ₂; 2 – 4 - линии по уравнению (1.6.13) для коэффициентов трения: f = 0.3; f = 0.4; f = 0.5)

Очевидно при этом, что допусти­мые значения не­разрушающих на­пряжений лежат внутри области диаграммы, ограниченной изображен- ными на рис. 1.6.6 пря­мыми, и теми же, но зеркально отображенными пря­мыми относительно прямой ₁ = ₂ (на рис. 1.6.6 не по­казаны). Как видно из анализа рис. 1.6.6 и 1.6.7, область до­пустимых (неразрушающих) значений главных напряжений ограничена сравнительно небольшими по величине значениями растягивающих усилий во включении (где ₁ и ₂ положительны).

Поскольку при одной и той же нагрузке трещина может перейти из включения (зародыша) в основной материал (зерновку) и прорезать все тело или остано­виться, то при дальнейшем увеличении нагрузки до­стигается новое критическое неустойчивое состоя­ние. Тогда диаграмма разрушения задается неравен­ством

max(₁, ₂) < К_1с( а)^-1/2.

-6,-6

6,-6

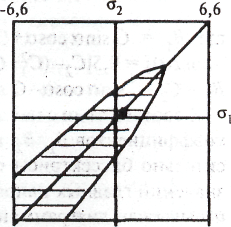
Рис.1.6.7. Область допустимых значений главных напряжений на берегах трещины (заштрихована)

Если берега трещины по-прежнему взаимодейст­вуют по закону кулонова трения, т.е. _ху  -k + _у⁰tg, где коэффициенты k и  отличаются от соответству­ющих постоянных для неразрушенного включения, то в таком случае коэффициент интенсивности на­пряжений равен [24]:

К_II = -(а₁)^1/2{2k + (₁ - ₂)sin2 -

- [₁ + ₂ + (₁ - ₂)соs2]tg}. (1.6.14)

Дифференцируя (1.6.14) по  и приравнивая получен­ную производную нулю, находят угол  = _, при ко­тором К_II максимально:

_ = (/2 - )/2 (0 < _ < /2); (1.6.15)

mах К_II = -(а₁)^1/2{2k - [₁ + ₂ - (₁ - ₂)/(2sin)]tg}.

Так как безопасная область для тела с трещинами скольжения определяется условием

mахК_II < К_IIc, (1.6.16)

то имеет место следующая диаграмма разрушения:

[₁ + ₂ - (₁ - ₂)/(2sin)]tg  К_IIc(а₁)^-1/2 + 2k(₁ > ₂). (1.6.17)

Преобразуем уравнение (1.6.17) к виду

[₁ + ₂ - (₁ - ₂)/(2sin)]tg  К_IIc + 2, (1.6.18)

где ₁ = k₁, ₂ = k₂, К_IIc = К_IIc(а₁)^-1/2/k, ₁, ₂, К_IIc - по-прежнему, безразмерные переменные. Опу­ская для простоты принятые по умолчанию чёрточки над безразмерными вели­чинами, преобразуют уравнение (1.6.18) к форме

₂ = [(К_IIc +2)/tg - ₁(1 - 0.5/sin)]/(1 + 0.5/sin). (1.6.19)

Количественное моделирование на основе уравне­ния (1.6.19) проводили для значений безразмерных па­раметров К_IIc = 1; f = 0.3; ₂ = 3. В результате полу­чили область допустимых (неразрушающих) значений главных напряжений (рис. 1.6.8) в виде двух симме­тричных относительно биссектрисы ₁ = ₂ треугольников (лежа­щий под биссект­рисой треугольник не показан). Если в теле зер­новки развивают­ся последователь­но процессы трещинообразования во включении (за­родыше) и в ос­новном материале (зерновке), то диа­грамма разруше­ния, схематически получающаяся пу­тем наложения ди­аграмм на рис. 1.6.5 и 1.6.6, может, быть изображена в ви­де, показанном на рис. 1.6.9.

Рис. 1.6.8. Границы области допустимых значений напряжений на берегах трещины (1 - линия по уравнению (1.6.19); линия ₂ - const; 3 - линия ₁ =_2с)

Рис. 1.6.9. Схема области допустимых неразрушающих напряжений в зерновке (заштрихована)

Поскольку в ре­альных условиях разрушение зер­новки, по-види­мому, происходит в результате разви­тия трещины в эн­досперме, то в таком случае следует считать, что локальное разруше­ние и образование трещины развивается в малой ок­рестности включения (в зародыше) в основном мате­риале композита эндосперм+оболочка.

Согласно общему методологическому подходу ме­ханики разрушения локальное разрушение опреде­ляется критериями вида F(К_I, К_II) = 0, где F - неко­торая функция, определяемая экспериментально. Поскольку опытных данных по определению этой функции пока недостаточно, то ее оценивают по двум предельным случаям, которые могут быть ис­следованы до конца аналитически: а) на продолже­нии включения образуется трещина отрыва, а коэф­фициент К_II = 0; б) на продолжении включения обра­зуется трещина сдвига, а коэффициент К_I = 0 [24].

В результате имеют диаграммы разрушения: в случае

а) - ₂(k₁ – 1)mах(₁,₂) - 2₁В  К_Ici(k₁ – 1)[₁(k₂ +1) + 2₂]/[2(а₁)^1/2];

в случае б) - ₁ - ₂ < К_IIci[2₁ + ₁(k₂ +1)/₂]/[₁(а₁)^1/2],

где новая константа К_IIci не совпадает с К_II и К_IIc. Результат наложения этих диаграмм показан на рис. 1.6.10. Полученную таким образом диаграмму принимают в качестве диаграммы разрушения, опи­сывающей начальное разрушение зерновки вблизи конца зародыша.

Сравнение диаграммы разрушения зародыша на рис. 1.6.9 и соответствующей диаграммы разрушения зерновки на рис. 1.6.10 дает возможность ответить на во­прос: какой из этих основных механизмов реализует­ся в каждом конкретном случае? В дальнейшем характер протека­ния процесса раз­рушения зависит от того, устойчив или неустойчив образовавшийся разрыв вблизи края зародыша. Если разрыв устойчив, то он будет развиваться до тех пор, пока нагрузка на зародыш не достигнет предельной величины, после чего зародыш разрушится и трещина станет неустойчивой. Для того чтобы ответить на этот вопрос нужно проводить дополнительное исследование.

Рис. 1.6.9. Схема области допустимых неразрушающих напряжений на основе модели локального разрушения зерновки в малой окрестности зародыша (заштрихована)

Практические расчеты процесса разрушения зер­новки под действием сил взаимодействия ее с други­ми частицами и стенками трубопровода осложнен из-за отсутствия достоверных сведений по таким па­раметрам зерновых материалов, как вязкость разру­шения К_c, коэффициент сцепления (адгезии) k₀, угол трения  и др. Если пользоваться соответствующими данными по материалам типа дерево, полистирол, графит, для которых значение вязкости разрушения находится в интервале 0.13 < К_с < 0.85 МПам^1/2 [25], то для зерновки примем ориентировочно К_с = 0.01 МПа м^1/2.

Для расчета значения напряжения _х и _у на гра­нице трещины (т.е. на границе зародыша) примем во внимание, что, согласно схеме А на рис. 1.6.1, контакт зерновки с поверхностью самотечного канала проис­ходит на сравнительно небольшом участке приведен­ным диаметром d₁, таком, что отношение (d₁/d)² — небольшая величина (d - приведенный диаметр зер­новки) (рис. 1.6.11).

Рис. 1.6.11. Схема к расчёту площади контакта зерновки с поверхностью самотёчного канала

С целью выразить главные напряжения ₁, ₂ че­рез напряжения _х и _у на основе формул (1.6.5) после­довательно имеют:

₁ + ₂ = _х + _у;

_у = [(_х + _у) - (2₁ - _х - _у)cos2]/2;

_ху = (2₁ - _х - _у)sin2/2;

(_х - _у)² + 4_ху² = (2₁ - _х - _у)²;

₁ = {(_х + _у) + [(_х - _у)² + 4_ху²]^1/2}/2;

₂ = {(_х + _у) -+ [(_х - _у)² + 4_ху²]^1/2}/2. (1.6.20)

Исходя из результатов количественного анализа гидродинамики потока зерносмеси, могут быть най­дены значения напряжений _х, _у, _ху. Если для про­стоты предположить, что основной вклад в напря­женное состояние на зерновке дают напряжения _х, _у, т.е. считать, что _х, _у >> _ху, то согласно (1.6.20) получают приближенно:

₁ = _у, ₂ = _х.

А если предполагать, что сами напряжения _х, _у определяются, главным образом, величиной гидростатического давления, то

_х = mghsin(d₁/d)², _у = mghсоs(d₁/d)²,

откуда, согласно

₂ = -₁tg.

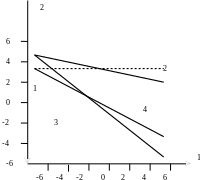
Рис. 1.6.12. Область допустимых значений неразрушающих напряжений зародыша (1 – линия по уравнению (1.6.19); 2 – линия ₂ = const; 2 – линия ₁ = ₂; 3 - линия ₂ = -₁tg)

Из анализа результатов расчетов (рис. 1.6.12) вытекает, что неразрушающие зародыш напряжения ограничены удвоенным (из-за симметрии области допустимых значений напряжений относительно биссектрисы ₁= ₂) значением величины отрезка прямой (1.6.22), заключенном внутри области допустимых значений напряжений ₁, ₂.

Рассмотрим пример.

Пусть толщина слоя зерносмеси h = 0.1 м, угол на­клона канала  = 30, плотность зер­новки ₁ = 1200 кг/м³, приведенный диаметр зерновки d = 3 мм, отношение приведенных диаметров зерновки и площади контакта зерновки с поверх­ностью самотечного канала (d₁/d) = 0.1; коэффициент вязкости разрушения К_с = 0.01 МПа м^1/2.

В таком случае, принимая во внимание зависи­мость k₀ = К_с(d)^1/2, для напряжений _х, _у (в безраз­мерной форме) получают _х = ₁ghsin(d/d₁)²/(6k₀) = ₁ghsin(d/d₁)²(d)^1/2/К_с = 12009.810²(1.2.140.003)^1/2sin3010^-4  0.6; _у = -₁ghсоs(d/d₁)²(d)^1/2/К_с = -1.02. Имея в виду зависимость ₁ = _у, ₂ = _х, в безразмерной форме находим прибли­женно: ₁ = _у = -1.02; ₂ = _х = 0.6.

Как видно по рис. 1.6.12, рассчитанные значения главных напряжений ₁ = ₂ расположены в области допустимых значений неразрушающих напряжений для зародыша. В то же время, если, например, тол­щина потока зерносмеси возрастет до 50 см, и, следо­вательно, значениями главных напряжений станут ₁ = -5.12; ₂ = 3, то мы, согласно рис. 1.6.12, уходим в область значений разрушающих напряжений заро­дыша, а значит, и разрушающих напряжений в зер­новке.

Если поток зерносмеси движется вниз самотеком по изогнутому участку канала радиусом R, то в до­полнение к действующему на поток гидростатичес­кому давлению следует прибавить центробежную си­лу, пропорциональную центростремительному уско­рению V²/R. Пусть, для простоты, центростремитель­ное ускорение в  раз больше ускорения силы тяжес­ти, т.е. V²/R = g и пусть направления этих ускорений взаимно ортогональны. Тогда результирующее уско­рение а_p (по модулю) составляет а_p = g(1 + ²)¹/². В та­ком случае рассчитанные в примерах значения глав­ных напряжений ₁, ₂ следует увеличить в (1 + ²)¹/² раз, что соответственно приведет к сужению облас­ти допустимых значений неразрушающих напря­жений в зерновке. Так, если, например, отноше­ние (V²/R)/g = 2 (и поэтому а_p = g(1 + ²)¹/² = 2.2), то при толщине слоя зерносмеси h = 0.1 м, угле на­клона канала  = 30 и тех же параметрах зерновки будем иметь ₁ = _у = -1.022.2 = -2.244; ₂ = _х = 0.62,2 = 1.32, а при толщине слоя зерносмеси h = 0.5 м получим ₁ = _у = -11.2; ₂ = _х = 6.6, что находится в области разрушающих напряжений за­родыша.

Данные теоретические исследования позволяют развить закономерности, полученные при рассмот­рении кинетики зерносмеси в самотечном трубопро­воде. Выведенные зависимости дают возможность проследить зарождение трещин и пути их развития в теле зерновки. Получены диаграммы границ области допустимых неразрушающих напряжений в теле зер­новки. Рассмотрены условия движения зернового потока по изогнутому участку самотечной системы.

Данные исследования могут быть полезны при проектировании самотечных систем в элеваторах, на крупяных заводах и в хранилищах семенного продук­та, т.е. там, где образование и развитие трещин в зер­новке приводит к снижению качества готового про­дукта или всхожести семян.