Анализ процесса измельчения зернопродуктов в межвальцовом зазоре
Обработка зерна вальцами является одним из основных процессов технологии зернопродуктов, в результате которого зерно в условиях сжатия и сдвига подвергается разрушению. Цель исследования - оценить предельные значения силовых и геометрических факторов процесса деструкции зерна в межвальцовом зазоре.
В основу теоретического анализа положена идеализированная модель, когда вальцы и зерновки считаются абсолютно твердыми цилиндрами. Кроме того, в целях упрощения анализа предполагают, что оси вальцов расположены по горизонтали (рис. 1.4.1, 1.4.2). В результате рассматривают задачу о равновесии одного или большего числа цилиндров (имитирующих зерновки), опирающихся на два цилиндра-вальца.
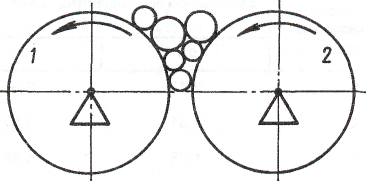
Рис. 1.4.1. Схема взаимодействия вальцов с зерносмесью
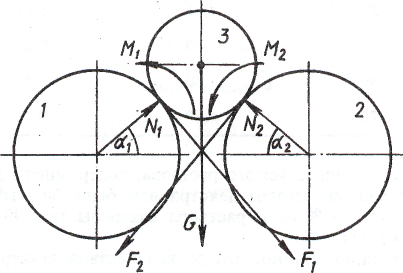
Рис. 1.4.2. Силовая схема нагрузок, действующих на зерновку в межвальцовом зазоре
В таком случае зерновка, испытывающая действие собственной массы и статического давления зерносмеси над нею (сила G на рис. 1.4.2), находится в состоянии предельного равновесия. При этом в левой точке опоры выполняются условия скольжения и качения, а в правой - условия качения. Тогда с учетом того, что вальцы вращаются в одном направлении, но с разными угловыми скоростями, силовая схема задачи имеет вид, представленный на рис. 1.4.2. В этом случае сила трения и моменты сил трения можно записать в следующем виде:
F1 = fN1, M1 = N1, M2 = N2, (1.4.1)
где f - коэффициент трения скольжения; - коэффициент трения качения; F1 - сила трения скольжения; M1 и M2 - моменты сил трения качения; N1 и N2 - реакции опоры [20].
Сила трения F2 в правой точке наряду со значениями N1 и N2 является искомой величиной. Условия равновесия плоской системы сил, представленные в виде равенства нулю проекции главного вектора по осям х и у и главного момента относительно центра зерновки, имеют вид [3]
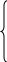
N1(cos1 + fsin1) – N2cos2 - F2sin2 = 0;
N1(cos1 - fsin1) + N2sin2 - F2cos2 = G; (1.4.2)
N1(f + k) + N2k - F2 = 0,
где k = /R, R - радиус цилиндра, имитирующего зерновку.
Решение системы уравнений (1.4.2) записывают согласно правилу Крамера
N1 = 1/, N2 = 2/, N3 = 3/,
где
= 2[(f + k)cos(/2) - (1 - f k) sin(/2)]cos(/2); = 1 + 2;
1 = -G(cos2 + k sin2);
2 = -G[cos1 + f sin2 - (f + k)sin2]; (1.4.4)
3 = -G[k(cos1 + f sin1) + (f + k) cos(/2)].
Так как по своему смыслу N1 величина положительная, а < 0, то из формул (1.4.3) и (1.4.4) вытекает условие [(f + k)cos(/2) - (1 - f k) sin(/2)]cos(/2) < 0, и в силу того, что <
tg2 > (f + k)/(1 - f), f k <1. (1.4.5)
В свою очередь, поскольку N2 > 0, то в дополнение к формуле (1.4.5) получают неравенство
cos1 + fsin1 > (f + k)sin2. (1.4.6)
Причем, как видно из формул (1.4.3) и (1.4.4), условие F2 > 0 удовлетворяется автоматически, если справедливо неравенство (1.4.5).
Таким образом, неравенства (1.4.5) и (1.4.6) являются необходимыми условиями существования предельного равновесия зерновки в зазоре между вальцами.
Принимая во внимание, что радиусы вальцов значительно больше радиуса цилиндра, моделирующего зерновку, считают, что 1 2 - небольшие величины. Поэтому, учитывая, что tg(/2) , cos1 1, sin1 1, sin2 2, на основании формул (1.4.5) и (1.4.6) приближенно получают
1 + 2 > 2(f + k)/(1 - f k), f k < 1,
(1.4.7)
1 + f 1 > (f + k)2.
Из анализа системы уравнений (1.4.7) следует, что областью решения системы неравенств является заштрихованный четырехугольник в плоскости 1, 2, ограниченный линиями = 1 + 2 = 2(f + k)/(1 - f k) и 1 + f 1 = (f + k)2 (рис. 1.4.3). Естественно, данное заключение справедливо, когда 1 и 2 невелики.
Рис. 1.4.3. Диаграмма допустимых значений углов контакта зерновки с вальцами
Для исследования напряженно-деформированного состояния зерновки важно знать величины N1, N2, F2. Для этого в тех же допущениях (справедливых в реальных условиях вальцовой обработки зерна) по значениям углов 1 и 2 в силу формул (1.4.3) и (1.4.4) приближенно имеют
= 2(f + k) - (1 - f k); 1 = -G(1 + k 2);
2 = -G[1 + f 2 - (f + k)2]; 3 = -G[k(1 + f 1) + f + k].
Кроме того, принимая во внимание неравенство fk < 1, и реальные значения коэффициентов трения, обосновывают в дальнейшем приближенные формулы
= 2(f + k); 1 = -G; 2 = -G; 3 = -G(2k + f).
Другой типичный случай предельного равновесия зерновок в зазоре между вальцами возникает, когда две или более зерновки образуют свод, изображенный в виде двух цилиндров с радиусами R1 и R2 (рис. 1.4.4). На этом рисунке для силовой схемы условия предельного равновесия по плоской системе сил для двух тел записывают в виде [3], [20]
N1cos1 + F1sin1 – N2cos2 - F2sin2 = 0;
N1sin1 - F1cos1 - N2sin2 - F2cos2 = G1;
F1R1 - F2R1 - N1 - N2 = 0; (1.4.8)
N2cos2 + F2sin2 – N3cos3 - F3sin3 = 0;
N2sin2 - F2cos2 + N3sin3 - F3cos3 = G2;
F2R2 - F3R2 + N2 + N3 = 0,
где величины N, F, G, R и имеют тот же смысл, что и ранее.
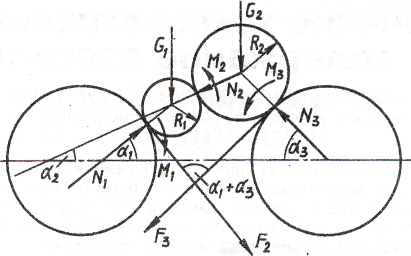
Рис. 1.4.4. Cиловая схема нагрузок на систему из двух зерновок в межвальцовом зазоре
Проводя анализ системы уравнений (1.4.8) по той же схеме, что и для системы (1.4.2), приходим к условиям предельного равновесия
или по двум одинаковым зерновкам, когда R1 = R2 = R,
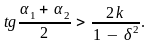(1.4.9)
В свою очередь, условие вытеснения пары частиц как единого свода, имеет вид
(1.4.10)
Поскольку, как правило, /R << f, k << f, то из сравнения неравенств (1.4.9) и (1.4.10) следует, что условие вытеснения зерновок из межвальцового зазора качением (формула (1.4.9) является менее жестким по сравнению с условием образования свода скольжением (формула (1.4.10)). Поэтому в реальных условиях обработки зерносмесей вальцами образование сводов из зерновок маловероятно.
Таким же образом могут быть исследованы и другие более сложные случаи предельного равновесия на основе модели качения для трех и большего числа цилиндров, имитирующих зерновки. Однако общий механизм разрушения свода в целом достаточно ясен.
Найденные на основе модели предельного равновесия силовые факторы, действующие на систему цилиндров, могут быть использованы в качестве исходных для расчета в дальнейшем условий разрушения в межвальцовом зазоре собственно зерновки.