1.3. Расчёт динамики измельчения частиц в дробилках ударного действия

В настоящее время для оценки эффективности из­мельчения материалов в химической, горнорудной и др. отраслях промышленности с помощью машин, реали­зующих ударное воздействие на тела, часто приме­няют статистический метод, основанный на допуще­нии о случайном взаимодействии и соударяющихся между собой тел и с рабочими органами дробилок удар­ного действия. С этой целью в качестве исходного кинетического уравнения, описывающего измельчение однородных тел, принимают зависимость скоростей из­менения крупности частиц от их среднего размера и аддитивной случайной составляющей в виде дельта-коррелированной функции времени, отражающей сто­хастический характер процесса измельчения. Для опре­деления средней скорости измельчения используют из­вестные эмпирические законы Кирпичева- Кика, Риттенгера, Бонда и др. [15]-[17]. Очевидно, что метод рас­чета эффективности измельчения таких материалов, как соль, мел, руда и др., на основе анализа статисти­ческих закономерностей изучаемого явления имеет огра­ниченную область применения и практически не позво­ляет учитывать многообразие факторов, обусловлива­ющих протекание процесса.

С помощью другого подхода, основанного на фено­менологических моделях измельчения при ударной об­работке (В. П. Горячкин, В. П. Ромадин, Н. Г. Капельзон и др.), получены формулы для расчета крити­ческих скоростей соударения, зависящих от тех или иных параметров процесса [модуля Юнга, плотности материала, предела прочности на растяжение (В. П. Го­рячкин) или коэффициента динамичности, пределов прочности при статической и динамической нагрузках, размера частицы (С. В. Мельников и др.)] [1].

Создание обоснованной физической модели ударной обработки различных материалов и математическое мо­делирование этого процесса с целью прогнозирования результатов измельчения с учетом основных геомет­рических и механических факторов является важной научно-технической проблемой. Ниже на основе теории динамического воздействия на тело в условиях фор­мирования трещин получены зависимости между дли­ной трещины, критической скоростью (скоростью разрушения) и основными параметрами ударной обработ­ки тела.

Если молоток (палец) дробилки, имеющий форму цилиндра, быстро вращается вокруг вертикальной оси, а измельчаемая частица имеет сферическую или мало отличающуюся от нее форму тела, то расчет динами­ческой нагрузки, приложенной со стороны пальца к телу, сводится к анализу ударного взаимодействия (на­пример, в рамках теории идеального удара) цилиндра с частицей сферической формы. В таком случае, пре­небрегая скоростью движения частицы от удара по сравнению с окружной скоростью пальца в точке со­ударения, можно показать, что скорость отскока

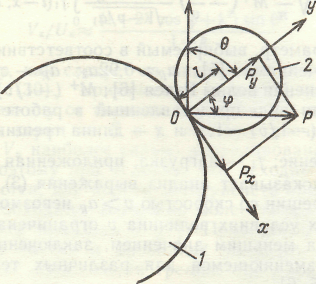
Рис. 1.3.1. Схема к расчёту ударного импульса при ударе молотка о частицу

U = V(1 + 2cos + ²)^1/2. (1.3.1)

где V - окружная скорость молотка в точке соударе­ния;  = (sin² + k²cos²)^1/2;  =  + ;  = агсtg(tg/k);  и  - соответственно угол падения и угол отражения; k - коэффициент восстановления.

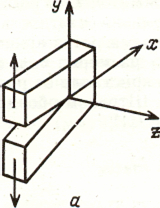
б

Рис. 1.3.2. Виды деформаций поверхности трещины в частице (а - поперечный отрыв, б - поперечный сдвиг).

Если т — масса частицы, то сообщаемый частице импульс при ударе

Р = тU(1 + 2cos + ²)^1/2,

откуда, проецируя по радиальному и касательному к поверхности частицы направлениям, получим

Р_х = Рsin, Р_у = cos. (1.3.2)

При этом предполагаем, что Р_у может иницииро­вать радиальную трещину, а Р_х является так назы­ваемой нагрузкой нормального отрыва. В дальнейшем считаем, что частица изотропна по механическим свой­ствам, а условия образования трещины в ней такие же, как и в безграничном теле. Тогда согласно дина­мической теории трещинообразования, исходя из фор­мулы Гриффитса, имеем в условиях реализации де­формаций нормального отрыва энергетическое соотно­шение [11],[18] (рис. 1.3.2, а):

(1.3.3)

где  - параметр Ламе; = 4 - (1 - ₂²)²; = v/a_1,2; а₁ и а₂ - скорость рас­пространения соответственно продольных и поперечных волн в теле; v - скорость развития трещины; К_I - коэффициент интенсивности напряжений при нормаль­ном отрыве; t - время;  - константа материала час­тицы, характеризующая поверхностную плотность энер­гии на разрыв.

Для случая нормального отрыва коэффициент ин­тенсивности напряжений принимают в форме [11]

(1.3.4)

где

(1.3.5)

(1.3.6)

h - параметр, выбираемый в соответствии с табличны­ми значениями [11]; а_R = 0.92а₂; а_R - скорость рас­пространения волны Рэлея [18]; - функция, имеющая вид, представленный в работе [11], причем lim_v = 1; l и х — длина трещины и текущее ее значение; f₁ - нагрузка, приложенная к телу.

Как показывает анализ выражения (1.3.3), распростра­нение трещин со скоростью v > a_R невозможно. В прак­тических условиях величина v ограничена не значени­ем a_R, а меньшим значением, заключенным в интер­вале, изменяющемся для различных тел от 0.2 до 0.5а₂ [11], [18].

Если f₁ = q₁(х)Н(t) (где (х) —дельта-функция Ди­рака, Н(t) —функция Хевисайда [19]) - сосредото­ченная ударная нагрузка, приложенная к частице в точке O перпендикулярно к оси у, т. е. в направлении, нормальном к трещине, то, исходя из уравнений (1.3.4), (1.3.6), получим:

. (1.3.7)

Тогда согласно формуле (1.3.7) и определению дельта-функции имеем [19]:

(1.3.8)

Если Т — время действия ударного импульса, а b - сторона куба, равновеликого сферической частице диа­метром d, т. е. b = d(/6)^1/3, то вследствие выражений (1.3.2) сосредоточенную ударную нагрузку на тело вычис­ляем по формуле:

(1.3.9)

где  — плотность частицы.

В таком случае в силу равенств (1.3.8), (1.3.9) получим:

. (1.3.10)

Таким образом, исходя из выражений (1.3.4), (1.3. 5) и (1.3.10), имеем

(1.3.11)

после подстановки которого в уравнение (1.3.3) находим:

(1.3.12)

где

(1.3.13)

Тогда согласно формуле (1.3.12) зависимость текущей длины трещины от скорости ее развития имеет вид:

(1.3.14)

Если определяется длина трещины l, развивающаяся в результате ударного импульса на частицу, то вы­числяется значение х при v 0. Тогда приходят к так называемому статическому критерию разрушения [11]. При этом имеющаяся в формуле (1.3.14) неопределен­ность вида 0/0 разрешается с помощью правила Лопиталя:

(1.3.15)

Если исходить из предположения, что частица раз­рушается при условии, когда длина трещины дости­гает размеров тела, т. е. l = d, то исходя из выра­жений (1.3.1), (1.3.15), можно получить формулу для рас­чета критической скорости соударения молотка с час­тицей, при которой происходит ее разрушение

(1.3.16)

С учетом того, что  = Е/[2( + 1)] (где Е и  — соответственно, модуль продольной упругости и коэффициент Пуассона), а продольная а₁ и поперечная а₂ скорости распространения волн деформации в теле связаны соотношением [14]

(1.3.17)

в силу выражений (1.3.15) - (1.3.17) находим:

, (1.3.18)

(1.3.19)

Полученная зависимость длины трещины от меха­нических параметров тела дает возможность вычис­лять скорость соударения молотка с частицей, при ко­торой образуются трещины заданной длины. Так, если требуется, чтобы в частице образовалась трещина дли­ной, равной, например, половине ее диаметра l = d, то в соответствии с формулой (1.3.19) должны иметь

(1.3.20)

или где вычисляется по выра­жению (1.3.19).

Очевидно, что сферическая частица диаметром d_, при повторном образовании в ней в результате удара двух трещин длиной d/2, разрушается. Поскольку после столкновения с молотком частица ударяется о деку со скоростью U = V(1 + 2cos + ²)^1/2, заключаем, что частица разрушается при последовательном соударе­нии с молотком и декой со скоростью

Пусть измельчению в молотковой дробилке подвер­гается поваренная соль при следующих параметрах: Е~10¹⁰ Па,  = 0.3 Н/м,  = 0.25, d = 510^-3 м,  = 2.510³ кг/м³ , k ~ 0.3, T = 510^-4 с,  = /4 [1], [14]. Тогда при расчете по формулам (1.3.19) и (1.3.20) получаем ~110 м/с, = 78 м/с. Расчетные значения по порядку примерно согласуются с найденными на практике при обработке поваренной соли в мо­лотковой дробилке ( ~ 60 - 70 м/с) [1].

Рассмотренная модель нормального отрыва при тре-щинообразовании в результате удара молотка о части­цу по форме, приближающейся к сферической, как показывает анализ формул (1.3.18) и (1.3.19), может быть использована в основном при косом ударе. Если со­ударение частицы с молотком близко к прямому (т. е. удар почти лобовой), то необходимо применять модели поперечного или продольного сдвига [11], [18] .

Пусть к частице, условно имеющей форму, близкую кубу со стороной b, приложен ударный импульс

P = P_x = mV(1 + k). (1.3.21)

Тогда, считая, что в частице развиваются лишь де­формации поперечного сдвига, по аналогии с выраже­нием (1.3.3) имеем энергетическое соотношение [11], [18] (см. рис. 1.3.2, б):

(1.3.22)

где K_II - коэффициент интенсивности напряжений при поперечном сдвиге, определяемый по формуле [11]:

. (1.3.23)

Принимая во внимание, что f₂ = q₂(х)Н(t) — удар­ная нагрузка, реализующая поперечный сдвиг в теле, в силу уравнения (1.3.23) получаем

(1.3.24)

причем, по аналогии с формулой (1.3.9), согласно равенству (1.3.21) находим

(1.3.25)

Тогда в соответствии с выражениями (1.3.22), (1.3.24), (1.3.25) имеем:

(1.3.26)

где

(1.3.27)

Так как в рамках поставленной задачи целью ана­лиза является оценка длины сформировавшейся тре­щины, т. е. расчет l при v  0, то, учитывая, что

вместо формулы (1.3.7) приближенно получаем

(1.3.28)

В таком случае, переходя в уравнении (1.3.26) к пре­делу при х  l, v  0 и принимая во внимание выра­жение (1.3.15), находим

(1.3.29)

Если предположить, что разрушение частицы про­исходит при образовании в ней трещины длиной l = b, то из формул (1.3.28) и (1.3.29) получим

(1.3.30)

Если считать, что полное или частичное разруше­ние частицы наступает при образовании в ней не ме­нее двух трещин размерами, равными половине реб­ра куба, т. е. при l = b/2, то, как и ранее, частица может делиться на фрагменты при V = 0.707V_к, где V_к находится по формуле (1.3.30). Расчеты по ней для кристаллов NaCl c ребром b = 510^-3 м для рассмот­ренного примера дают V_к = 62 м/с, что находится в области наблюдаемых на практике критических ско­ростей удара, при которых отмечалось разрушение час­тиц соли [1] .

Сравнение результатов расчетов критических ско­ростей на основе моделей «нормальный отрыв» и «по­перечный сдвиг» показывает, что, как и следовало ожидать, критическая скорость при косом ударе («нор­мальный отрыв») выше соответствующей скорости при ударе, близком к прямому («поперечный сдвиг»), при­чем, согласно выражениям (1.3.19) и (1.3.30)

V_к/U_к 

Поскольку, как вытекает из анализа структуры формул (1.3.19) и (1.3.30), критическая скорость зависит по линейному закону от периода импульса Т и по закону квадратного корня из Е и , точность расчетов значений V_к и U_к наиболее сильно зависит от величины Т. Поэтому при условии, что исходный размер частиц известен, для корректного расчета критической скорости необходимо возможно более точное определение периода импульса Т. Проведенный анализ измельчения частиц в дробилках ударного действия как результат образования трещин при ударном воздействии на частицы справедлив в рамках допуще­ний, принятых при обосновании исходной механической модели (изотропность свойств, безграничность размеров тела, его хрупкость, идеальный характер процесса соударения тел и др.).