1.2. Анализ эффективности процесса измельчения частиц в дробилках ударного действия

В настоящее время для оцен­ки эффективности процессов из­мельчения сыпучих материалов широко используют статистиче­ские методы, основанные на концепции о случайном ха­рактере взаимодействия соуда­ряющихся частиц и рабочих ор­ганов дробилок. В качестве ис­ходного уравнения, описываю­щего кинетику измельчения крупности частиц и их средним размером и аддитивной состав­ляющей как дельта-коррелиро­ванной функции времени, отра­жающей как дельта-коррелиро­ванной функции времени, отра­жающей стохастический харак­тер процесса измельчения. Для нахождения средней скорости измельчения используют из­вестные законы разрушения ма­териалов Кирпичева Кика, Риттингера, Бонда и др. [7] – [9]. При этом очевидно, что метод расчета эффективности процес­са измельчения ударом таких сыпучих материалов, как соль, мел, руда и др., на основании анализа статистических законо­мерностей изучаемого явления имеет сравнительно ограничен­ную область применения и прак­тически не дает возможности учитывать многообразие факто­ров, обусловливающих разви­тие этого процесса. С другой стороны, с помощью подхода, основанного на феноменологи­ческих моделях процесса удар­ного измельчения, найдены фор­мулы для расчета критических скоростей соударения в зависи­мости от параметров процесса обработки (модуля Юнга, плот­ности материала, прочности на растяжение и др.) или от коэф­фициента динамичности, преде­ла прочности при статической и динамической нагрузках, раз­мера частицы [7]. Однако про­цесс измельчения сыпучих материалов в молотковых дробилках до сих пор недостаточно изу­чен, что отрицательно сказы­вается на практике проектиро­вания и изготовления машин, действие которых основано на принципе ударного измельчения материала. В связи с этим ак­туальна задача углубленного теоретического и эксперимен­тального анализа кинетики из­мельчения частиц в корпусе молотковой дробилки с целью обоснования оптимальных гео­метрических размеров машины и рациональных физико-меха­нических параметров этого про­цесса.

В применяемых для измельче­ния сыпучих материалов в хи­мической, горнорудной и дру­гих отраслях промышленности дробилках основным рабочим органом являются молотковый ротор из насаженных на гори­зонтальный вал ярусов радиально расположенных молот­ков и дека - внутренняя орифленная цилиндрическая поверх­ность. Поступающий из бунке­ра материал сначала подвер­гается удару со стороны вра­щающегося с большой угловой скоростью молотка, а затем от­скочившая от молотка частица материала ударяется либо о де­ку, либо о другую (другие) частицы. Причем наиболее эф­фективным с точки зрения раз­рушения частицы ударом, раз­вивающимся при больших ско­ростях соударения, чем при уда­ре молотка о частицу, являет­ся повторный удар ее (если она предварительно не разру­шилась) о деку. Дальнейшее пе­ремещение частиц в корпусе дробилки практически теряет детерминированный характер и становится хаотическим с пре­имущественным движением в окружном направлении в виде измельченного закрученного разрыхленного слоя, увлекае­мого молотками.

Таким образом, процесс из­мельчения сыпучего материал в корпусе дробилки можно услов­но разбить на два этапа: сна­чала происходит обработка ча­стиц при соударении их с мо­лотком и декой (или другими частицами), а затем продукты дробления подвергаются обра­ботке истиранием в условиях развития сдвиговых напряже­ний между частицами и непод­вижными органами дробилки (декой, ситом). Оценку эффек­тивности процесса измельчения материала в корпусе дробилки будем проводить путем анализа кинетики частиц в результате соударения их с молотком и де­кой.

При исследовании кинетики измельчения материала на пер­вом этапе обработки его в кор­пусе дробилки примем следую­щие допущения: частицы имеют сферическую форму, а моло­ток - цилиндрическую (при­мерно такую форму в процессе эксплуатации молоток прини­мает в результате многих удар­ных столкновений с частица­ми); скоростью частиц до соуда­рения с молотком, влиянием си­лы тяжести и аэродинамиче­ского сопротивления на их движение, а также отклонением молотка при ударе пренебрега­ем. Кроме того, считаем, что удар частиц о молоток яв­ляется центральным, а частицы при ударе их о рабочие орга­ны дробилки и соударениях между собой не проскальзыва­ют.

При анализе ударного взаи­модействия частицы с молотком целесообразно предположить, что молоток неподвижен, а ча­стица ударяется о него с гори­зонтальной скоростью v = v₀ (здесь v₀ =  ;  - угловая скорость ротора;  - радиаль­ное расстояние от оси враще­ния ротора до места контакта частицы и молотка ( рис. 1.2.1)).

Для определения скоро­сти частицы после удара будем исходить из того, что в точке А касательные и нормальные со­ставляющие скорости частицы (по модулю) до и после соуда­рения связаны соотношениями (1.1.1) - (1.1.4) и вытекающими из них зависимостями

Рис. 1.2.1. К расчёту кинетики частицы при соударении её с молотком и декой

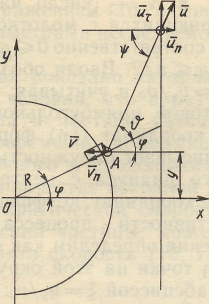
и_х = v₀(1 + cos),

и_у = v₀ sin, (1.2.1)

где  = (sin² + k²cos²)^1/2,  =  + .

С учетом значения нормаль­ной составляющей u_n скорости частицы после соударения с мо­лотком и полученной опытным путем или теоретически зависимости функции распределения Ф(v_п) = N/n₀ относительного числа частиц, неразрушенных в результате удара (здесь N - число неразрушенных частиц; п₀ - число частиц до удара), может быть рассчитано относи­тельное число частиц, разру­шенных в результате последова­тельного соударения их с молот­ком и декой. Действительно, со­бытия «частица разрушилась при ударе о молоток», «частица разрушилась после отскока от молотка и соударения с декой» и «частица не разрушилась пос­ле соударений с молотком и де­кой» образуют полную группу событии. Поэтому, рассчитывая вероятность наступления по­следнего события как резуль­тата совместного появления двух событий: «частица не разрушилась после соударения с молотком» и «частица оста­лась целой после удара о деку», по теореме умножения вероят­ностей может быть найдена вероятность разрушения части­цы либо после удара о молоток, либо после соударения с декой. Пусть Ф_v(v_п) и Ф_и(и_п) — фун­кции распределения относи­тельного числа не разрушенных частиц при ударе о молоток и при соударении с декой (оче­видно, что зависимость Ф обус­ловлена формой и материалом молотка и деки). Согласно смыслу функции распределения Ф изменяется в пределах от 0 до 1 и является убывающей функ­цией нормальной составляющей скорости соударения. В таком случае согласно теореме умно­жения вероятностей относи­тельное число частиц, отскочив­ших от молотка по дуге d и не разрушившихся при соударении с декой, составляет [4, 10]

(1.2.2)

где - элемент угла паде­ния частицы на молоток (при условии, что процесс соударе­ния обращен); п₁ - число ча­стиц, соударяющихся с молот­ком по дуге ₁; ₁ - предель­ное значение угла падения, при котором отскочившая от молот­ка частица еще достигает деку. Очевидно, что равенство (1.2.2) выполняется при значениях , удовлетворяющих согласно выражению (1.1.3) условию (ри­с. 1.2.1)

 +  < _max,

где угол _max < /2 обусловлен геометрией рабочей полости дробилки.

Входящая в равенство (1.2.2) нормальная составляющая ско­рости и_п зависит от угла между вектором скорости частицы, от­скочившей от молотка, и нор­малью к поверхности деки. В связи со сложностью определе­ния этого угла с небольшой по­грешностью заменяем его на  =  + , т. е. на угол между скоростью 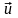и нормалью к пло­скости, перпендикулярной пло­скости чертежа (рис. 1.2.1). В таком случае с учетом формул (1.2.1) и (1.2.4) получим

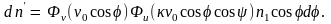(1.2.3)

Интегрируя выражение (1.2.3) по  в пределах от 0 до ₁ = _max, найдем число частиц, не разрушившихся при ударе о деку,

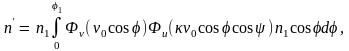(1.2.4)

где ₁ = _max = _max - _max; углы  и  связаны зависимостью (1.1.3).

К рассчитанному по выраже­нию (1.2.4) числу частиц, не раз­рушившихся при последова­тельном соударении с молотком и декой и сталкивающихся с молотком по дуге 0    _max, следует добавить число частиц, соударяющихся только с молот­ком, не разрушающихся при ударе и не достигающих деки, т. е. частиц, соприкасающихся с молотком по дуге ₁ <   /2 (косой удар). По аналогии с выражением (1.2.6) число таких частиц

При этом очевидно, что

n₁ = yN/R = Nsin₁,

n₂ = (R – y)N/R = Ncos₁.

В таком случае общее число частиц, не разрушенных при соударении с молотком и декой, N₁ = п' + п", а число разрушенных частиц N - N₁ = N – (п' + п"). В качестве коэффи­циента эффективности процесса измельчения частиц зерна в мо­лотковой дробилке принимаем

 = [N – (п' + п")]/N = 1 - (nsin₁)/n₁ - (ncos₁)/n₂ =

= 1 - -

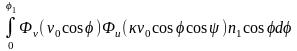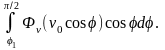- (1.2.5)

Проверка формулы (1.2.5) на асимптотику для предельных значений скорости соударе­ния v₀ частицы и молотка по­казывает, что с учетом пре­дельных значений характери­стических функций

Ф_v(0) = 1; Ф_u(0)=1; lim_vФ_v(v) = 0; lim_uФ_u(u) = 0;

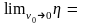1 - - = 1 -

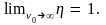
Иначе говоря, эффективность процесса при малых скоростях соударения стремится к нулю, а при больших скоростях соуда­рения - к единице, как и следо­вало ожидать исходя из смысла коэффициента эффективности  процесса измельчения. С другой стороны, рассматривая случай абсолютно неупругого соударе­ния частицы с молотком (счи­тая, что коэффициент восста­новления k  0) , в соответствии с выражением (1.1.3) получим   /2, т. е. при абсолютно неупругом соударении частица отскакивает от молотка по ка­сательной в месте контакта. В этом случае частица не достигает деки, и в формуле (1.2.5) следует полагать ₁ = 0, т. е. для случая абсолютно неупругого соударения

 = 1 -

При этом по-прежнему

0,

Исследование измельчения сыпучего материала в корпусе дробилки, основанное на анали­зе вероятностной модели явле­ний соударения частиц с рабо­чими органами измельчающей машины, базируется на том, что предполагаются известными статистические вероятностные характеристики процесса в виде функций распределения по кри­тическим скоростям относитель­ного числа разрушенных при ударах частиц. Вследствие то­го, что собственно процесс разрушения частиц при соуда­рении с рабочими органами дро­билки рассматривается как яв­ление, носящее случайный ха­рактер, такой подход к анализу эффективности процесса из­мельчения зерна условно назо­вем стохастическим. При от­сутствии статистических сведе­ний о процессе к анализу исследуемой проблемы может быть применен подход, который назовем детерминированным. Этот подход основан на ис­пользовании при анализе про­цесса измельчения частиц уда­ром формул расчета критиче­ских значений скоростей разру­шения, полученных, например, с помощью динамической тео­рии разрушения (в частности, исходя из теории разрушения тел как результата развития в них трещин под действием ударных нагрузок [11], [12]).

Если известна скорость раз­рушения v_к частицы при пря­мом ударе (критическая ско­рость), то допуская, что v_к < v₀ = , на основании уравнения (1.1.1) найдем предельное значе­ние угла падения  = _к, при ко­тором нормальная проекция скорости частицы равна кри­тической:

_к = arcos(v_к/v₀). (1.2.6)

Согласно определению кри­тической скорости все частицы, соударяющиеся с молотком по углу 0    _к, разрушаются при ударе. При этом относи­тельное число таких частиц среди всех других, соприка­сающихся с молотком,

 = р = n/N = y/R =

= sin_к = [1 - (v_к/v₀)²]^1/2, (1.2.7)

где п' и N — число частиц, соударяющихся с молотком по дугам соответственно 0    _к и 0    /2. Вводя обозначе­ние  = v_к/v₀ и учитывая, что в декартовой прямоугольной си­стеме координат () формула (1.2.7) описывает окружность еди­ничного радиуса с центром в начале координат, коэффициент эффективности процесса из­мельчения определим как орди­нату  точки на этой окружно­сти с абсциссой  = v_к/v₀.

Поскольку частицы, соприка­сающиеся с молотком по углу падения  > ₁ имеют нормаль­ную составляющую скорости, меньшую, чем v_к, они могут разрушиться лишь при соударе­нии с декой. Предельный угол падения частицы на деку со­гласно выражениям (1.1.1) - (1.1.3) можно определить из выраже­ния

u_к = v₀cos,

откуда

• = _к = arcos[u_к/(v₀)]

и

_к  + аrсtg(tg_к /k) = _к, (1.2.8)

где и_к - критическая скорость прямого удара частицы о деку.

Необходимо отметить, что критический угол _к следует определять численным путем как корень трансцендентного уравнения (1.2.10). Если при этом _к < _к, то очевидно, что деки достигают лишь фрагменты час­тиц, разрушенных при соударе­нии с молотком. В свою оче­редь, согласно принятой схеме частицы, соударяющиеся с мо­лотком по дуге  <   ", разрушаются при ударе о деку. Относительное число таких частиц

р = n/N = (y - y)/R = sin_к - _к.

Поскольку общее число раз­рушенных частиц N₁ = п' + п", может быть найдет коэффи­циент эффективности процесса измельчения при детерминиро­ванном подходе к анализу это­го процесса:

 = (п' + п")/N = _к.

Таким образом, получена формула простого вида, в кото­рой  зависит только от угла _к, связанного в соответствии с выражением (1.2.8) с основными параметрами исследуемого про­цесса.

Как показано авторами [12], при условии, что в результате удара в частице развиваются одновременно деформации по­перечного и продольного сдви­га, в качестве исходной расчет­ной критической скорости раз­рушения частицы, может быть принята скорость [13], [14]

v_к = (1.2.9)

где  - время действия ударного импульса, с;  - плотность частицы, кг/м³;  - константа, характеризующая поверхностную плотность энергии на разрыв, Н/м; Е - модуль упругости, Па;  - модуль Пуассона; а - размер части­цы, м.

Критическую скорость части­цы при ударе о деку можно вычислить по формуле

u_к = v_к/(1 + k),

где v_к рассчитывается по вы­ражению (1.2.9).

Предложенную методику рас­чета коэффициента эффектив­ности процесса измельчения используем для количественно­го анализа процесса дробле­ния кристаллов поваренной соли NаСl (Е=10¹⁰ Па;  = 0.3 Н/м;  = 0.25; а = 510^-3 м;  = 2.510³ кг/м³; k = 0.3 [13] ). Полагая ско­рость соударения кристалла NаСl с молотком v₀ = 60 м/с, продолжительность ударного импульса  = 510^-4 с, най­дем [1]

v_к/v₀ =

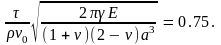
В таком случае в соответ­ствии с формулой (1.2.6) _к  40°. Предполагая, что нор­мальная составляющая скоро­сти соударения частицы с декой меньше критической скорости прямого удара, т. е. частицы разрушаются лишь в процессе соударения их с молотком (_к < _к), для рассматриваемо­го примера коэффициент эффек­тивности процесса измельчения можно определить по формуле

 = р = sin_к = sin40° = 0.64 = 64 %.

Таким образом, на основании теории удара обоснована методика количественной оценки процесса измельчения соли в молотковой дробилке.