Движение заряженной частицы мясокостного сырья в электрическом поле переменной напряжённости, с учётом кинетики зарядки

Движение частицы в неод­нородном электрическом поле с учетом кинетики зарядки частицы наибо­лее полно моделирует ее поведение в реальных условиях. Вместе с тем, поскольку данное движение является и наиболее сложным для теоретического анализа, то эту задачу можно решить только при соответствующих упрощающих допущениях. В качестве таких допущений принимаем предположение о линейном характере зависимости напряженности поля от расстояния до коронного разряда. Зависимость заряда частицы от времени, как и в предыдущем разделе, будем рассчитывать по формуле Потенье [44], а силу сопротивления - по формуле (2.3.7). Кроме того, движение частицы в горизонтальном направлении, т.е. по вектору напряженности поля, считаем безынерционным (рис. 2.3.2).

С учетом принятых допущений напряженность поля рассчитываем согласно зависимости

E = E₀(1 - х)i, (2.3.28)

где  = (E₀ – E₁)/L > 0 – множитель пропорциональности, градиент напряженность электрического поля; E₀, E₁ - соответственно, напряженность электрического поля на стенке х = 0 и х = L, L - ширина канала (рис. 2.3.2).

Тогда согласно (2.3.3), (2.3.28) сила Кулона представляется в виде

F_к = Q_m(1 - х)²t/(t + t_з)i, (2.3.29)

где

Q_m = 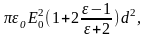Н; t_з = с. (2.3.30)

Проецируя векторное уравнение (2.3.1) на оси координат, c учётом (2.3.2) - (2.3.4), (2.3.29) получим

mdV_x/dt = Q_m(1 - х)²t/(t + t_з) - k₁V_xv , (2.3.31)

mdV_y/dt =-mg – k₁(V_y - U) v , (2.3.32)

где, по-прежнему, v = V_y - U < 0 – скорость витания, k₁ - имеет тот же смысл, что в предыдущем разделе.

Разделив обе части уравнений (2.3.31), (2.3.32) на m, будем иметь

dV_x/dt = Q_уд(1 - х)²t/(t + t_з) - kV_xv , (2.3.33)

dV_y/dt =-g – k(V_y - U) v , (2.3.34)

где Q_уд = Q_m/m, k = k₁/m.

Вводя, по-прежнему, скорость v = V_y – U  0 V_x > 0, систему уравнений (2.3.33), (2.3.34) преобразуем к виду

dV_x/dt = Q_уд(1 - х)²t/(t + t_з) + kV_xv, (2.3.35)

dv/dt =-g + kv². (2.3.36)

Причём, если уравнение (2.3.36) совпадает по форме с (2.3.13), то уравнение (2.3.35) по сравнению с (2.3.12) имеет более сложный вид, практически исключающий исследование данного уравнения в аналитической форме.

В целях упрощения расчётов сделаем допущение о том, что движение частицы в горизонтальном направлении является квазистационарным, т.е. будем полагать dV_x/dt  0. В результате чего вместо системы уравнений (2.3.35), (2.3.36) получим приближенно

Q_уд(1 - х)²t/(t + t_з) + kV_xv = 0, (2.3.37)

dv/dt =-g + kv². (2.3.38)

При этом решением дифференциального уравнения (2.3.38), удовлетворяющего начальному условию (2.3.9), по-прежнему, является (2.3.17).

Учитывая, что согласно с (2.3.17)

v = -( V_y – U) =

и, кроме того, V_x = dх/dt, уравнение (2.3.37) переписываем в виде

Q_уд(1 - х)²t/(t + t_з) + k(dх/dt) = 0,

откуда, разделяя переменные и принимая во внимание соотношение kb = а/2, будем иметь

(2.3.39)

Проводя в (2.3.39) интегрирование, получим

(2.3.40)

где С – произвольная постоянная.

Согласуя (2.3.40) с начальным условием х = 0 при t = 0, будем иметь С = а, и поэтому приходим к частному решению

x(t) = [1-Ф^-1(t)]/, (2.3.41)

где

Ф(t) = . (2.3.42)

а

2

4

3

1

б

в

4

3

2

1

Рис. 2.3.5

Зависимости ординаты у (м) частицы от её абсциссы х (м) при плотности частицы ₁ = 1200 кг/м³, коэффициенте сопротивления с_у = 1.2 “лёгкие частицы”

(а: d =1 мм; 1 - U = 3 м/с, Е = 10⁵ В/м ; 2 - U = 3 м/с, Е = 210⁵ В/м; 3 - U = 6 м/с, Е = 10⁵ В/м; 4 - U = 6 м/с, Е = 210⁵ В/м;

б: U = 6 м/с; 1 - d = 1 мм, Е = 10⁵ В/м; 2 - d = 1 мм, Е = 210⁵ В/м; 3 - d = 2 мм, Е = 10⁵ В/м; 4 - d = 2 мм, Е = 210⁵ В/м;

в: Е = 10⁵ В/м; 1 - d =1 мм, U = 3 м/с; 2 - d =1 мм, U = 6 м/с;

3 - d = 2 мм, U = 3 м/с; 4 - d = 2 мм, U = 6 м/с)

Таким образом, на основе формул (2.3.25), (2.3.42) в рамках принятых допущений построены параметрические по t уравнения движения час-

а

5

4

3

2

1

б

5

4

3

2

1

1

Рис. 2.3.6

Зависимости ординаты у (м) частицы от её абсциссы х (м) при плотности частицы ₁ = 1200 кг/м³, градиенте напряжённости  = 0.5 В/м², коэффициенте сопротивления с_у = 0.8 (“тяжёлые частицы”)

(а: d = 1 мм; 1 - U =1 м/c, Е₀ = 10⁵ В/м; 2 - U = 3 м/с, Е₀ = 10⁵ В/м ; 3 - - U = 1 м/с, Е₀ = 210⁵ В/м; 4 - U = 3 м/с, Е₀ = 210⁵ В/м; 5 - U = 2 м/с, Е₀ = 10⁵ В/м;

б: d = 2 мм; 1 - U =1 м/c, Е₀ = 10⁵ В/м; 2 - U = 3 м/с, Е₀ = 10⁵ В/м ; 3 - U = 1 м/с, Е₀ = 210⁵ В/м; 4 - U = 3 м/с, Е₀ = 210⁵ В/м; 5 - U = 2 м/с, Е₀ = 10⁵ В/м)

тицы в неод­нородном электрическом поле с учетом кинетики зарядки частицы. При этом, как и в предыдущем разделе в силу того, что уравнения (2.3.25), (2.3.42) не допускают явного исключения параметра t, для получения зависимости между координатами точки приходится использовать те же математические итеративные процедуры, что и раньше.

Построенные на базе (2.3.25), (2.3.42) в виде графиков (рис. 2.3.5, 2.3.6) зависимости ординаты у частицы от её абсциссы х для близких к реальным значениям параметров процесса - диаметру d частицы, плотности _п частицы и _в газа, коэффициенту сопротивления с_у, скорости U потоке воздуха, напряжённости Е электрического поля, градиенту напряжённости  = (E₀ – E₁)/L > 0 выявляют качественное и количественное согласие их с графиками на рис. 2.3.4, 2.3.5. В то же время вследствие наличия перепада напряжённости  отмечается и некоторая особенность кинематики точки при различных значениях . Так, например, согласно расчёту, для значений режимных параметров E₀ = 10⁵ В/м,  = 0.25 В/м², d = 10^-3 м, U = 3 м/с частица достигает стенку x = L = 0.12 м за Т= 0.02 с, поднявшись на h = 1.7 см, а при тех же значениях параметров E₀, d, U, но для  = 0.5 В/м², соответственно, имеем Т= 0.018 с, h = 1.5 см. Что соответствует физической стороне исследуемого процесса.

Поскольку обрабатываемая сыпучая смесь обычно является полидисперсной, то обоснованный количественный анализ эффективности процесса сепарирования взвеси может быть проведен лишь на базе достоверных данных по гранулометрическому составу компонентов смеси – в данном случае - “тяжёлых” и “лёгких” частиц. Для чего в рассматриваемой проблеме целесообразно использовать, например, массовую характеристическую функцию F(d) = m(d)/m₀, где m(d) - масса частиц размером больше d в некотором объёме, m₀ – масса частиц в том же объёме.

а

1

4

5

3

2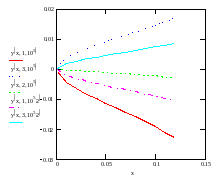

б

5

4

3

2

1

Рис. 2.3.7

Зависимости ординаты у (м) частицы от её абсциссы х (м) при плотности частицы ₁ = 1200 кг/м³, градиенте напряжённости  = 0.25 В/м², коэффициенте сопротивления с_у = 0.8 (“тяжёлые частицы”)

(а: d = 1 мм; 1 - U =1 м/c, Е₀ = 10⁵ В/м; 2 - U = 3 м/с, Е₀ = 10⁵ В/м ; 3 - U = 1 м/с, Е₀ = 210⁵ В/м; 4 - U = 3 м/с, Е₀ = 210⁵ В/м; 5 - U = 2 м/с, Е₀ = 10⁵ В/м;

б: d = 2 мм; 1 - U =1 м/c, Е₀ = 10⁵ В/м; 2 - U = 3 м/с, Е₀ = 10⁵ В/м ; 3 - U = 1 м/с, Е₀ = 210⁵ В/м; 4 - U = 3 м/с, Е₀ = 210⁵ В/м; 5 - U = 2 м/с, Е₀ = 10⁵ В/м)

В качестве коэффициента эффективности осаждения (условно) принимаем

 = [m₀ - m₁]/m₀, (2.3.43)

где m₁ – масса частиц, ушедших с потоком воздуха (в относ).

Очевидно, что величина  соответствующего коэффициента эффективности уноса (для частиц, отошедших в относ) связана с коэффициентом  зависимостью  = 1 - .

Пусть исходный полидисперсный по составу сыпучий материал в виде частиц мясокостного сырья равномерно перемешан на входе в канал и его примерная характеристическая функция F(d) (рис. 2.3.8) представлена зависимостью

1 при  < 1 мм

F(d) = (1 - d)/9 + 1 при 1    10 мм (2.3.44)

0 при  > 10 мм.

Рис. 2.3.8

Примерная характеристическая функция распределения частиц мясокостного сырья

И пусть его движение в рабочем канале сепаратора в дальнейшем определяется совместным действием на смесь воздушного потока, силы тяжести и электрического поля переменной напряжённости. В таком случае если параметрами процесса являются: Е₀ = 10⁵ В/м;  = 0.5 В/м²; d = 2 мм; U = 2 м/с, L = 0.15 м, то согласно данным рис. 6, б, критический диаметр частицы d_кр  2 мм.

Тогда в соответствии с уравнением (2.3.44) будем иметь F(d) = F(2) =

= (1 - 2)/9 + 1 = 1 - 0.11 = 0.89. Иначе говоря, в соответствии с расчётом в сепараторе осаждается около 89 % и уходит в относ 11 % от исходного объёма данного вида обрабатываемого мясокостного сырья.

Поэтому, как видно согласно проведенному по рассмотренному примеру количественному анализу, с помощью соответствующего набора режимных параметров пневмосепарирования может быть

Таким образом,

- на основе анализа кинетики изолированной заряженной частицы, такой как замороженное измельченное мясокостное сырьё, перемещающейся под действием электростатического поля и силы тяжести в восходящем воздушном потоке, получены расчётные зависимости по кинематическим характеристикам движения частицы;

- на базе геометрических и физико-механических параметров процесса сепарирования, в зависимости от показателя аэродинамического сопротивления, по найденным кинематических характеристик движения заряженной частицы в силовых полях различной структуры проведено количественное моделирование данных характеристик с целью обоснования критической траектории и критического диаметра частицы;

- исходя из заданного для исходного сырья массового распределения частиц по их размерам в виде функции распределения и основных режимных параметров процесса сепарирования получено выражение коэффициентов эффективности осаждения и уноса как функций критического диаметра частицы по фракциям сырья для воздушного электростатического сепаратора, что создаёт предпосылки эффективно прогнозировать процесс разделения на компоненты смеси типа замороженное измельченное мясокостное сырьё.

УДК 664.7

ОБОЗНАЧЕНИЯ

с_у - аэродинамический коэффициент сопротивления;

d - диаметр частицы, м;

d_к - критический диаметр частицы, м;

Е, Е₀, Е₁ - напряжённость электрического поля, В/м;

е – заряд электрона, Кл;

F – характеристическая функция;

g - ускорение свободного падения, м/с²;

L –ширина канала, м;

m - масса частицы, кг;

n₀ - концентрация ионов, 1/м³;

q – заряд частицы, Кл;

S – площадь миделевого сечения, м²;

Т - время осаждения частицы, с;

t - время, с;

х, у - декартовы координаты, м;

U - скорость потока, м/c;

V_x, V_y – проекции абсолютной скорости частицы по осям х и у, м/c;

v - скорость витания частицы, м/c;

 - коэффициент эффективности осаждения;

 - коэффициента уноса;

 - диэлектрическая проницаемость материала частицы;

 – подвижность ионов, м²/(Вс).

 - коэффициент эффективности уноса;

 - градиент напряженность электрического поля, В/м²;

_в – плотность воздуха, кг/м³;

_т - плотность частицы, кг/м³.