Контрольная работа №4

Теория функций комплексного переменного.

Уравнения математической физики

Теория вероятности

Математическая статистика

Введение.

Общий курс высшей математики, изучаемой студентами-заочниками инженерно-технических и технологических специальностей, состоит из аналитической геометрии с элементами линейной алгебры, математического анализа, элементов теории вероятности и математической статистики.

Этот курс ставит основной своей задачей сообщить студенту сведения о высшей математике, необходимые для успешного изучения общетеоретических и специальных дисциплин, и также развить навыки логического мышления.

Учебный материал по курсу высшей математики распределен на пять первых семестров. В конце каждого семестра предусмотрен зачет или экзамен по изученным разделам математики. Соответственно этим разделам студенты выполняют контрольные работы согласно учебному плану своей специальности.

Основной формой обучения студента-заочника является самостоятельная работа над учебным материалом. Лекции, практические, индивидуальные межсессионные занятия призваны помочь им в самостоятельной работе и выполнении контрольных работ.

Работа студента-заочника над учебным материалом по математики состоит из следующих элементов: слушание лекций, участие в практических занятиях, участие в межсессионных индивидуальных занятиях, изучение материала по учебникам, решение задач, ответы на вопросы для самоконтроля, выполнение контрольных работ (1-5 в семестр), сдача зачетов и экзаменов.

Настоящий сборник содержит все задания для выполнения контрольных работ по высшей математике а также ставит цель помочь студенту-заочнику самостоятельно работать над учебным материалом по высшей математике, в нем перечислена литература, рекомендованная для самостоятельного изучения материала, содержится программа по всему курсу, методика изучения и решения типовых вариантов контрольных работ.

Требования к оформлению контрольных работ

Контрольная работа должна выполняться студентом в соответствии с номером варианта, который определяется двумя последними цифрами номера зачетной книжки студента.

При оформлении контрольной работы необходимо учитывать следующие требования:

1. на титульном листе указать номер варианта;

2. контрольные работы оформлять, оставляя поля для замечаний преподавателя;

3. условия задач необходимо записывать полностью. Если задание имеет общую формулировку, его условие необходимо переписать, подставляя числовые значения, соответствующие номеру варианта;

4. решения заданий оформлять аккуратно, приводить достаточное количество пояснений, делать необходимые рисунки.

Контрольную работу необходимо сдать за 10 дней до начала экзаменационной сессии, в противном случае студент не будет допущен до зачета или экзамена.

Решение типового варианта

Пример 1. Указать область, определяемую условиями , , .

Решение. Неравенство , равносильное неравенству , определяет внешность круга (включая границу) радиусом 1 с центром в точке . Неравенство или определяет полосу, заключенную между прямыми и . Неравенство или определяет полосу, заключенную между прямыми и .

Пример 2. Найти аналитическую функцию по ее заданной действительной части .

Р

.

ешение. Для определения мнимой части воспользуемся условиями Коши-Римана. Так как , то согласно первому условию . Отсюда, интегрируя по y, находим:

Д ля определения функции воспользуемся вторым условием Коши-Римана. Так как , а , то . Отсюда и , где . Поэтому . Находим функцию :

Пример 3. Решить задачу Коши

,

.

Решение. По условию , поэтому, пользуясь формулой , получим

Пример 4. Дан тонкий однородный стержень длиной , изолированный от внешнего пространства, начальная температура которого равна . Концы стержня поддерживаются при температуре, равной нулю. Определить температуру стержня в момент .

Решение. Математически данная задача сводится к решению следующей смешанной задачи для одномерного однородного уравнения теплопроводности:

,

,

,

решение которой дается формулой , где при . Вычислим :

,

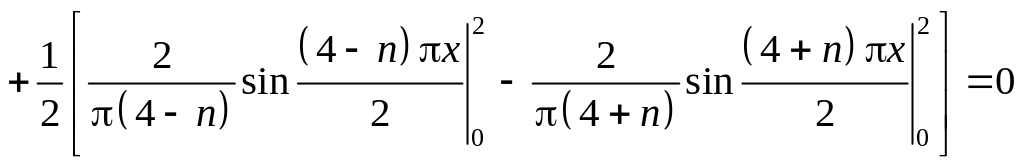при и . Если и , получим

,

.

Замечание. Коэффициенты можно определить из тождества

.

Отсюда в силу линейной независимости системы функций получим , , для .

Пример 5. Найти решение уравнения Лапласа в области, заключенной между двумя концентрическими окружностями радиусов и с центрами в начале координат, удовлетворяющее граничным условиям .

Решение. Запишем граничные условия в полярных координатах: первое не изменится, второе примет вид

.

Решение задачи ищем в виде . Удовлетворим граничным условиям:

,

.

Отсюда

для ;

для ,

для .

З этих двух серий соотношений (линейной алгебраической системы уравнений) определяем коэффициенты:

а) ,

б) ,

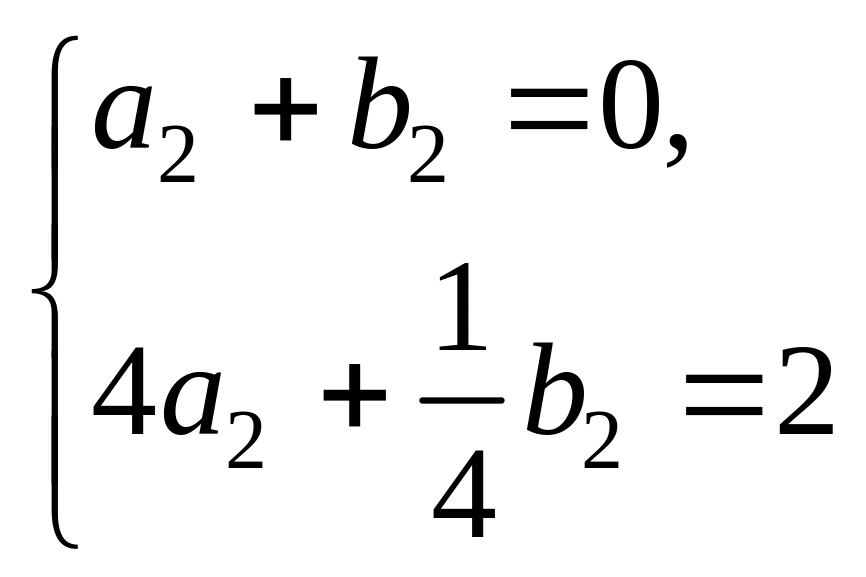
в) все остальные коэффициенты равны нулю.

Итак,

,

или в декартовых координатах , ,

.

Задача 5.1. В партии из 10 деталей 7 стандартных. Найти вероятность того, что среди шести взятых наудачу деталей 4 стандартных (событие ).

Решение. Общее число возможных элементарных исходов испытания равно числу способов, которыми можно извлечь 6 деталей из 10, т. е. числу сочетаний из 10 элементов по 6 элементов: .

Определим число исходов, благоприятствующих событию А. Четыре стандартные детали можно взять из семи стандартных деталей способами. Остальные 6-4=2 детали должны быть нестандартными. Их можно взять из 10-7=3 нестандартных деталей способами. Таким образом, число благоприятствующих исходов равно .

Следовательно, искомая вероятность равна

.

Задача 6.

6.1. Консультационный пункт университета получает пакеты с контрольными работами из городов А, В и С. Вероятность получения пакета из города А равна 0,7, из города В – 0,2. Найти вероятность того, что очередной пакет будет получен из города С.

Решение. События «пакет получен из города А», «пакет получен из города В», «пакет получен из города С» образуют полную группу, поэтому сумма вероятностей этих событий равна единице: . Отсюда искомая вероятность равна: .

6.2. Вероятность того, что расход электроэнергии в продолжение одних суток не превысит установленной нормы, равна . Найти вероятность того, что в ближайшие 6 суток расход электроэнергии в течение 4 суток не превысит нормы.

Решение. Вероятность нормального расхода электроэнергии в продолжение каждых из 6 суток постоянна и равна . Следовательно, вероятность перерасхода электроэнергии в каждые сутки также постоянна и равна .

Искомая вероятность по формуле Бернулли равна

.

Задача 6.3. Вероятность того, что деталь не прошла проверку ОТК, равна . Найти вероятность того, что среди случайно отобранных деталей окажется не проверенных от до деталей.

Решение. Точное значение искомой вероятности можно найти с помощью формулы Бернулли, однако это приводит к громоздким вычисления, поэтому воспользуемся интегральной теоремой Муавра-Лапласа:

, , .

Так как , то

, ,

поэтому

.

Пользуясь таблицей значений функции Лапласа, находим

.

Задача 7.

7.1. При установившемся технологическом процессе предприятие выпускает своих изделий первым сортом и вторым сортом. Найти закон распределения случайной величины – числа изделий первого сорта из взятых наугад четырех изделий. Вычислить математическое ожидание , дисперсию и среднее квадратическое отклонение этой случайной величины.

Решение. Очевидно, что случайная величина может принимать следующие возможные значения: 0,1,2,3,4. вероятности этих значений вычислим по формуле Бернулли:

,

,

,

,

.

Проверка: , т. е. вычисления выполнены правильно.

Итак, закон распределения случайной величины :

	0	1	2	3	4

Вычислим математическое ожидание, дисперсию и среднее квадратическое отклонение:

;

;

.

7.2. Непрерывная случайная величина задана плотностью вероятностей

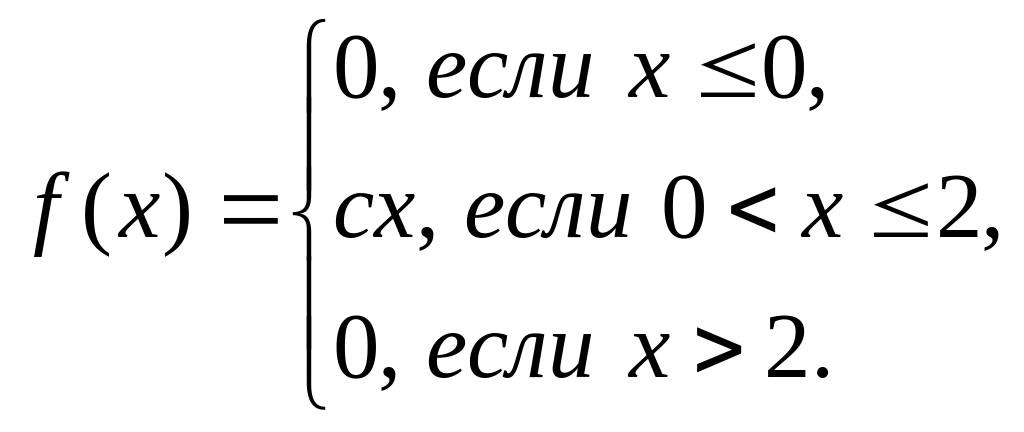
Найти: а) постоянный параметр с; б) функцию распределения ;в) вероятность того, что в результате испытания примет значение из интервала (0,5; 1,5); г) математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины .

Решение.

а) Определим параметр с из условия :

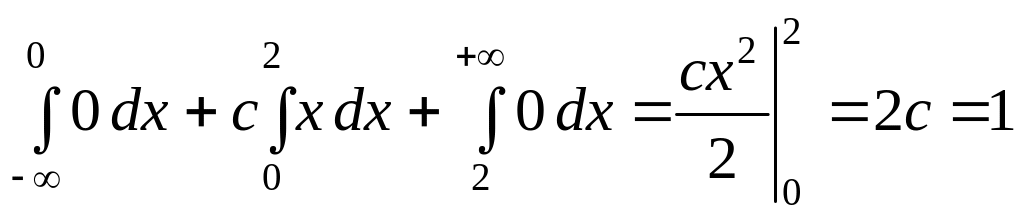, т е. .

б) Найдем функцию распределения :

1) если , то ;

2) если , то ;

3) если , то .

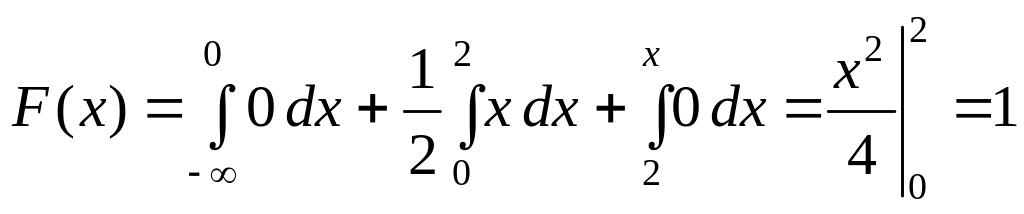Следовательно

в)

г) ;

;

.

Задача 8. Случайная величина имеет нормальное распределение с выборочным средним и средним квадратическим отклонением . Найти доверительные интервалы для оценки неизвестного математического ожидания , если объем выборки и задана надежность (доверительная вероятность) оценки .

Решение. Воспользуемся рабочей формулой

,

где точность оценки .

По таблице функции Лапласа (см. приложение) из соотношения найдем . Определим точность оценки

.

Следовательно, доверительный интервал будет

т. е. .

Отв.: .

Замечание. Так как – постоянная величина, то было бы ошибочным написать , ибо либо заключена в этом интервале (тогда событие достоверно и вероятность равна единице), либо нет (это событие невозможно, вероятность его равна нулю).

Надежность указывает, сто если произведено достаточное число выборок, то 95% из них определяет такие доверительные интервалы, в которых параметр действительно заключен; лишь в 5% случаев он может выйти за границы доверительного интервала.