3. Методы измерения связей между количественными признаками

Методы изучения функциональных связей:

1) балансовый метод;

2) индексный метод (см. тема 9).

В статистике широко используют балансовые построения, как метод анализа связей и пропорций в экономике. Статистический баланс представляет собой систему показателей, которая состоит из двух сумм абсолютных величин, связанных между собой знаком равенства:

А+С=D+E

Посредством балансов связывают в единую систему абсолютные величины, характеризующие движение ресурсов. Простейшим балансом такого рода является баланс оборотных средств какой-либо организации. Суммы показателей в нём образуют начальный и конечный остатки, поступление и расход. Эта система может быть изображена таким балансовым равенством:

остаток начальный + поступление – расход = остаток конечный

Приведённая балансовая формула характеризует процесс движения оборотных средств и показывает взаимосвязь и пропорции отдельных элементов этого процесса. Поступление и расход должны быть в определённом соответствии. Если это соответствие нарушается, то резко меняется удельный вес запасов к концу периода по сравнению с начальным. Поэтому нормальный ход процесса требует определённой пропорциональности между всеми элементами баланса.

Методы изучения корреляционных взаимосвязей

• Между атрибутивными признаками – метод взаимной сопряжённости.

• Между количественно – варьирующими:

1) метод параллельных рядов;

2) графический метод (корреляционного поля);

3) табличный метод (корреляционной таблицы);

4) метод аналитических группировок;

5) корреляционно – регрессионный анализ

4. Регрессионный анализ

Корреляционно-регрессионный анализ предполагает установление аналитической формы связи (регрессионный анализ) и измерение тесноты, направления связи (корреляционный анализ).

Наиболее часто для характеристики регрессии используют следующие типы функций:

Линейная регрессия

У_х = а₀ + а₁Х или У_{1, 2,3 …п} = а₀ + а₁Х₁ + а₂Х₂ + … + а_пХ_п

Параболическая связь

У_х = а₀ + а₁Х + а₂Х² или У_{1, 2, 3…п} = а₀ + а₁Х₁² + а₂Х₂² + … + а_пХ_п²

Гиперболическая связь

У_х = а₀ + а₁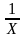 или У_{1, 2, 3…п} = а₀ +

Полулогарифмическая кривая

У_х = а₀ + а₁lg Х

Логистическая кривая

У_х =

Показательная функция

У_х = а₀а₁^Х или У_{1, 2, 3…п} = е^{А0 + А1Х1 +А2Х2 + … АпХп}

Степенная функция

У_х = а₀Х^а1 или У_{1, 2, 3,…п} = а₀Х₁^А1· Х₂^А2 · Х₃^А3….Х_п^Ап

Оценка параметров уравнений регрессии (а₀, а₁, а₂…а_п) осуществляется методом наименьших квадратов. Сущность его заключается в минимизации суммы квадратов отклонений эмпирических (фактических) значений результативного признака от теоретических, полученных по выбранному уравнению регрессии.

Каждый коэффициент регрессии показывает, на сколько в среднем изменится величина результативного признака в случае изменения факторного признака на единицу при фиксированном положении остальных факторов.

Значимость коэффициентов регрессии осуществляется с помощью t- критерия Стьюдента:

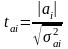
входные параметры: α, ν = п – к - 1,

Если t_факт > t_табл, то параметр модели принимается значимым

где

σ²_аi – дисперсия коэффициентов регрессии;

α – уровень значимости критерия о равенстве нулю параметров;

ν – число степеней свободы;

п - количество единиц совокупности;

к – число факторных признаков в уравнении;

Адекватность корреляционно-регрессионной модели осуществляется с помощью F- критерия Фишера:

входные параметры: α, ν₁ = к, ν₂ = п-к-1,

где

r²_УХ – коэффициенты детерминации.

Если F_факт > F_табл, то можно утверждать о надежности построенного уравнения.

Для характеристики корреляции применяют показатели тесноты связи между явлениями. Они различаются в зависимости от формы и вида связи.