8. Основные законы и соотношения алгебры логики.
Наиболее простые и необходимые связи между мыслями выражаются в основных формально-логических законах. При решении логических задач часто приходится упрощать формулы. Упрощение формул в булевой алгебре производится на основе эквивалентных преобразований, опирающихся на основные законы.
Основные законы логики |
|||
1 |
|
2 |
|
3 |
|
4 |
|
Свойства констант |
|||
5 |
|
6 |
|
7 |
|
8 |
|
9 |
|
10 |
|
Законы идемпотентности |
|||
11 |
|
12 |
|
Законы коммутативности |
|||
13 |
|
14 |
|
Законы ассоциативности |
|||
15 |
|
16 |
|
Законы дистрибутивности |
|||
17 |
|
18 |
|
Законы поглощения |
|||
19 |
|
20 |
|
Законы де Моргана |
|||
21 |
|
22 |
|
Замена операции импликация |
|||
23 |
|
||
Замена операции эквиваленция |
|||
25 |
|
||
9. Цифровые элементы.
Всякое устройство ЭВМ, выполняющее арифметический действия над двоичными числами, можно рассматривать как функциональный преобразователь. Преобразователи, которые могут, получая сигналы об истинности отдельных простых высказываний, обработать их и в результате выдать значение, называются логическими элементами.
Значение функции |
Название операции |
Обозначение функции |
Название элемента |
Условное обозначение элемента |
|||
0 |
0 |
1 |
1 |
||||
0 |
1 |
0 |
1 |
||||
0 |
0 |
0 |
1 |
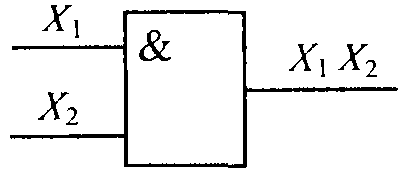
конъюнкция |
|
И |
|
0 |
1 |
1 |
1 |
дизъюнкция |
|
ИЛИ |
|
1 |
0 |
0 |
0 |
стрелка Пирса |
|
НЕ ИЛИ |
|
1 |
0 |
0 |
1 |
эквивалентность |
|
Эквивалентность |
|
1 |
0 |
1 |
1 |
импликация |
|
ЕСЛИ, ТО |
|
1 |
1 |
0 |
0 |
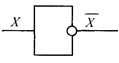
отрицание |
|
НЕ |
|
0 |
1 |
1 |
0 |
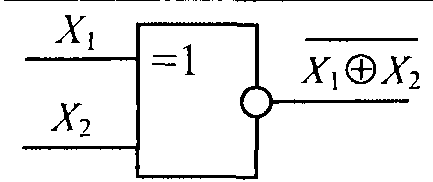
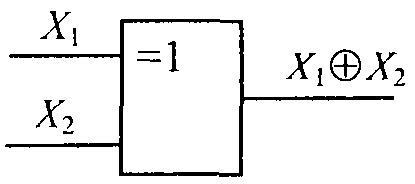
отрицание эквивалентности |
|
Исключающее ИЛИ |
|
1 |
1 |
1 |
0 |
штрих Шиффера |
|
НЕ И |
|
