6. Формы логических функций.
Различают несколько способов задания функций алгебры логики, основными из которых являются:
Т
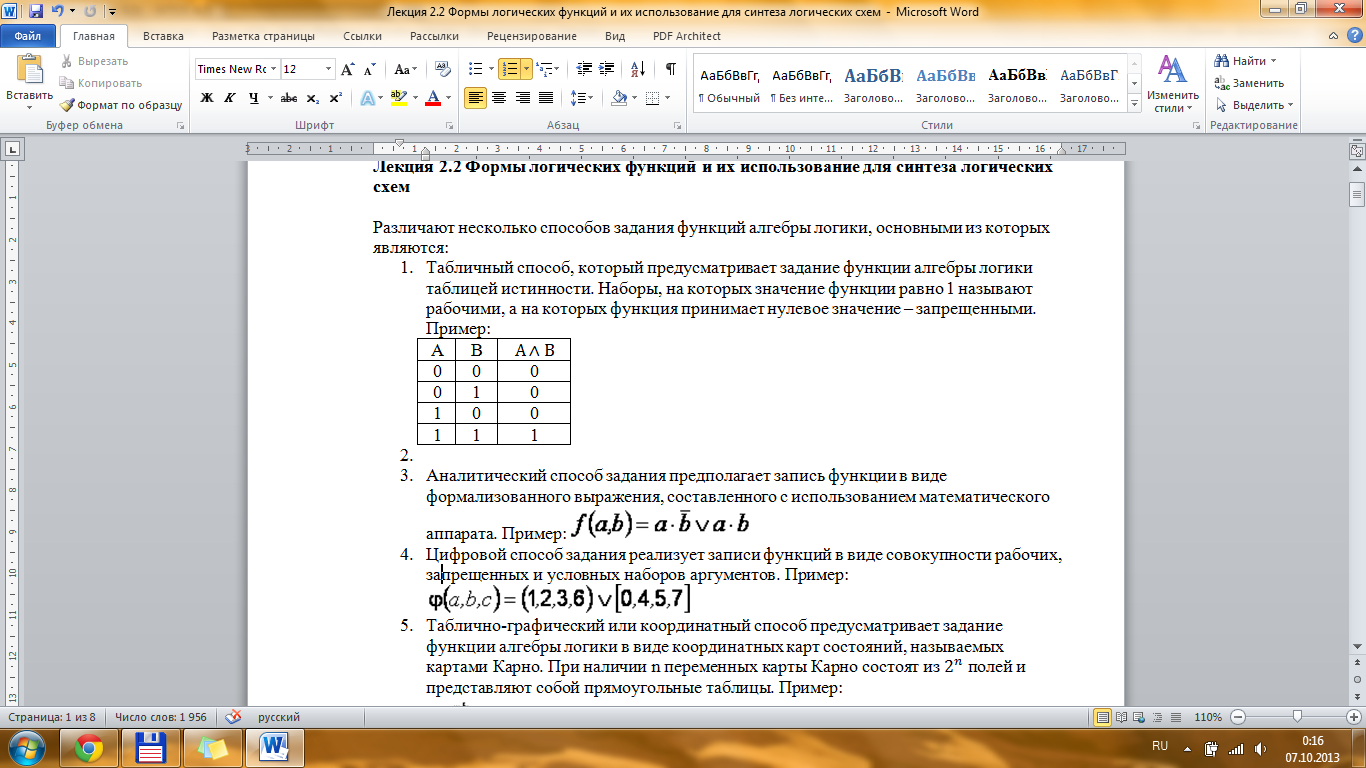абличный
способ, который предусматривает задание
функции алгебры логики таблицей
истинности. Наборы, на которых значение
функции равно 1 называют рабочими, а на
которых функция принимает нулевое
значение – запрещенными.
А
Рис 1. Табличный способ
налитический способ задания предполагает запись функции в виде формализованного выражения, составленного с использованием математического аппарата. Пример: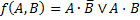
Цифровой способ задания реализует записи функций в виде совокупности рабочих, запрещенных и условных наборов аргументов. Пример:
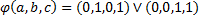
Т
Рис 2. Таблично-графический способ
аблично-графический или координатный способ предусматривает задание функции алгебры логики в виде координатных карт состояний, называемых картами Карно. При наличии n переменных карты Карно состоят из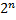
полей и представляют собой прямоугольные
таблицы.
Графический способ задания предусматривает изображение функции в виде n-мерной геометрической фигуры, вершинам которой соответствуют наборы значений аргументов данной функции.
7. Алгоритм заполнения таблицы истинности.
Таблица – это один из способов задания функций алгебры логики. Табличный способ, который предусматривает задание функции алгебры логики таблицей истинности. Наборы, на которых значение функции равно 1 называют рабочими, а на которых функция принимает нулевое значение – запрещенными.
Алгоритм заполнения таблицы истинности:
Пусть функция состоит из n простых.
Тогда число строк в таблице истинности 2n (два значения: 0 или 1).
Число столбцов в таблице равно сумме числа переменных и числа различных логических операций, входящих в функцию.
Заполняем первые n столбцов для переменных (перебираем все возможные значения). Таким образом, все возможные варианты учтены и никакие два не совпадают.
Заполняем таблицу истинности в соответствии с определениями логических операций.
Пример. Построить таблицу истинности
для функции 
А |
В |
С |
|
|
|
|
|
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
