
- •Задание №8 вариант №10
- •Кинематическая схема редуктора
- •Режим нагружения
- •1 Кинематический и энергетический расчет редуктора
- •1.1 Разбивка общего передаточного отношения
- •1.2 Определение частот вращения валов
- •2.2 Определение допускаемых напряжений
- •2.3 Определение допускаемых напряжений изгиба
- •2.4 Расчет цилиндрической передачи (2-я ступень)
- •2.4.1 Определение основных геометрических параметров цилиндрической передачи.
- •2.4.2 Проверочный расчет передачи на контактную прочность.
- •2.5.2 Проверочный расчет передачи
- •2.5 Расчет конической передачи
- •2.5.1Определение основных геометрических параметров конической передачи.
- •5 Предварительный выбор подшипников на валы
2.3 Определение допускаемых напряжений изгиба
Допускаемые напряжения изгиба для зубчатых колёс определим по формуле:
[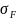 ]
=
]
=
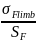 ·KFL
·KFC
·KFL
·KFC
Flimb j - базовый предел выносливости по изгибу.
SF - коэффициент безопасности.
KHLj - коэффициент долговечности,
Согласно рекомендации [1] определяем Flimb и SF:
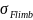 =
800 МПа.
=
800 МПа.
SF 1,65 2,3, принимаем SF 1,975.
Базовое число циклов NF0 4106
Расчетное число циклов перемены напряжений определим по формуле: NFEj 60×Cj ×nj ×th×KFE
KFE=19×1×0,55+0,879×1,15×0,25+0,839×1,2×0,2=0,67686
для колеса z1:
NFE1 60××1×12000,68 3,1·106
для колес z2:
NFE2 60××2×1200 ×18,6106
Так как NFE1,NFE2, >NFO , то KFL1 =KFL2 =1
Поскольку зуб работает одной стороной, то KFL1 =KFL2 =1
Коэффициент,учитывающий двустороннее нагружения зуба : KFC=1
Определяем [ ]:
[
]1
=
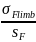 ·KFC·KFL=
·KFC·KFL=
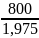 · 1·1 = 405,06 МПа.
· 1·1 = 405,06 МПа.
В качестве допускаемых напряжений изгиба для передачи принимаем меньшее значение из двух полученных:
[ ]1= 1368,5 МПа.
[ ]1 = = 405,06 МПа.
2.4 Расчет цилиндрической передачи (2-я ступень)
2.4.1 Определение основных геометрических параметров цилиндрической передачи.
Определяем межосевое расстояние:
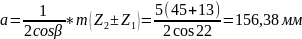 .
.
aw ≥ a =157
задаем коэффициент формы зуба эквивалентного колеса согласно [1]:
торцевой
модуль:
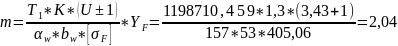
округляем по ГОСТ, но не меньше mmin = 2,5 мм
Принимаем модуль m = 5 мм.
где
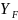 –
предварительно принятый коэффициент
формы зуба.
–
предварительно принятый коэффициент
формы зуба.
Для
шестой степени точности
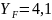 .
.
Число
зубьев шестерни:
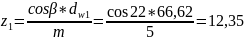
Тогда
число зубьев колеса:
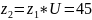 .
.
Уточняем размеры диаметров делительных окружностей:
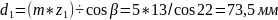
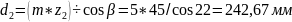 .
.
2.4.2 Проверочный расчет передачи на контактную прочность.
Проверим зубчатую передачу на выносливость от действия контактных напряжений.
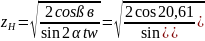
ZƐ=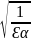 =
=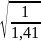 =
0,84
=
0,84
d1 = (m×Z1) ÷ cosβ = (5×13) ÷cos22= 70,10 мм.
da1 = d1+2m(1+X1-∆y) = 70,10+2×5(1+0,08-0,126)=79,64
db1 = d1 ·cosαt = 65,25
d2= (m×Z2) ÷ cosβ =(5×45)÷cos22=242,67 мм
da2 = d2 +2m (1+X2-∆y) = 242,67+2×5(1+0,24-0,126)=253,81
db2= d2·cos αt = 242, 67 ·cos 21,43 = 225,89
Уточним величину коэффициента динамической нагрузки [1]. Для этого рассчитываем окружную скорость в зацеплении:
V=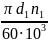 =
=
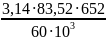 = 2,85 м/с
= 2,85 м/с
и назначаем 6-ю степень точности [1].
коэффициент динамической нагрузки Кv=1
KHα=1,04
Kβ =1,22
по таблице №7
=1,22
по таблице №7
Kβ=1,22
Кн=
KHα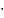 Kβ
Кv=1,04
Kβ
Кv=1,04
 1,22
1=1,27
1,22
1=1,27
Ψвd=вw÷dm1=53÷83,52=0,63
Коэффициент торцевого перекрытия Ɛα определим по формуле:
Ɛα
=
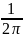 (z1
·tgαa1
± z2·tgαa2
– (z2±z1)tgαtw)
(z1
·tgαa1
± z2·tgαa2
– (z2±z1)tgαtw)
Ɛα = ( 13tg34,98 + 45·tg27,12 – 58·tg21,88) = 1,41.
Коэффициент αβ
αβ=вwsinβ÷3,14m=1,22
aw=157
αtw=arcos(a×(cosαt /aw)=21,88
αt=arctg(tg20/cos22)=21,43
2.5.2 Проверочный расчет передачи
zv1=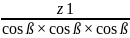 =
=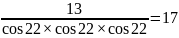 ;
;
=
275 · zH
·zE
·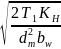
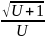 <[
<[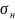 ]1=1368,5
МПа
]1=1368,5
МПа
=
275 ·1,65·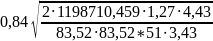 = 1267,21 МПа
= 1267,21 МПа
 =
=
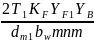 ≤ [
]1
≤ [
]1
σF1=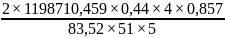 =169,
79≤
[
]1
=169,
79≤
[
]1
