§6. Закон збереження кількості руху. Реактивний рух. Центр мас

Розглянемо систему матеріальних точок, які взаємодіють між собою. Сили, з якими взаємодіють між собою точки даної системи, називають внутрішніми силами і позначають: . Нехай на систему, крім внутрішніх сил, діють зовнішні сили .

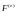Зовнішні сили – це сили, з якими на матеріальні точки даної системи діють тіла, які не належать цій системі (зовнішні тіла).

Запишемо другий закон Ньютона для кожної точки, врахувавши, що на кожну точку діють як зовнішні, так і внутрішні сили:

.

(6.14)

де – імпульс матеріальної точки номер якої n;

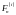– векторна сума внутрішніх сил, прикладених до n-ної точки;

– векторна сума зовнішніх сил, які діють на точку з номером n.

Додавши почленно рівняння системи (6.14), отримаємо:

.

(6.15)

де – геометрична сума зовнішніх сил

– геометрична сума внутрішніх сил, що діють у даній системі.

Але 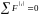, бо, згідно з третім законом Ньютона, , де – сила, з якою точка з номером k діє на точку з номером i, – сила, з якою i-та точка діє на k-ту точку.

З урахуванням сказаного рівняння (6.15) можна записати у вигляді:

.

(6.16)

Врахувавши те , що 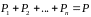, рівняння (6.16) запишемо у вигляді:

.

(6.17)

Рівняння (6.17) є математичним виразом другого закону Ньютона для системи матеріальних точок. Перша похідна за часом від імпульсу системи матеріальних точок дорівнює геометричній сумі всіх зовнішніх сил, які діють на систему матеріальних точок.

Якщо геометрична сума зовнішніх сил, які діють на систему матеріальних точок, дорівнює нулю, то рівняння (6.17) набере вигляду: , а це означає, що

.

(6.18)

Рівняння (6.18) є математичним виразом закону збереження імпульсу. Закон збереження імпульсу можна сформулювати так: Імпульс системи (кількість руху) матеріальних точок залишається сталим, якщо сума всіх зовнішніх сил, що діють на систему, дорівнює нулю.

Закон збереження імпульсу для замкнутих систем формулюють ще й так: Сумарний імпульс замкненої системи матеріальних точок залишається сталим під час будь-яких взаємодій між точками даної системи.

Закон збереження імпульсу є одним із фундаментальних законів фізики. Він виконується як для макроскопічних сил, так і для мікрочастинок.

Прикладом виконання закону збереження кількості руху може бути реактивний рух. Принцип реактивного руху покладений в основу побудови реактивних двигунів. Також використовують цей принцип руху деякі тварини. Наприклад, кальмари і медузи пересуваються, викидаючи воду зі спеціальних порожнин. Швидкість кальмарів може досягати 50-80 км/год. (рис. 6.1)

Рис .6.4

2. Центр мас. Поступальний рух всіх точок тіла або системи тіл можна замінити рухом однієї точки, в якій, як вважають, сконцентрована вся маса системи. Цю точку називають центром маси системи (Рис. 6.5, . Центром мас системи матеріальних точок, називають точку, до якої б стиснулась система під час рівномірного її стискання.

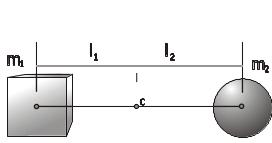
Рис. 6.5

Нехай система складається з n матеріальних точок масою . Положення точок визначається координатами . В цьому випадку центр мас системи знаходиться в точці з координатами, що визначаються за формулою (6.19):

.

(6.19)

де – координати центра мас.

У замкненій системі імпульс та швидкість центра мас залишаються сталими.

Якщо на систему матеріальних точок (кожне тіло можна розглядати як сукупність матеріальних точок) діють зовнішні сили , то центр мас системи рухається як матеріальна точка, маса якої дорівнює сумарній масі всієї системи, до якої прикладена сила, що дорівнює геометричній сумі всіх зовнішніх сил, що діють на систему:

.

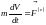(6.20)

Наведене твердження називається теоремою про рух центра мас.