§4. Плоский рух твердого тіла

Рух твердого тіла називають плоским, якщо всі його точки мають швидкості,вектори яких паралельні деякій площині. Плоский рух широко використовується в т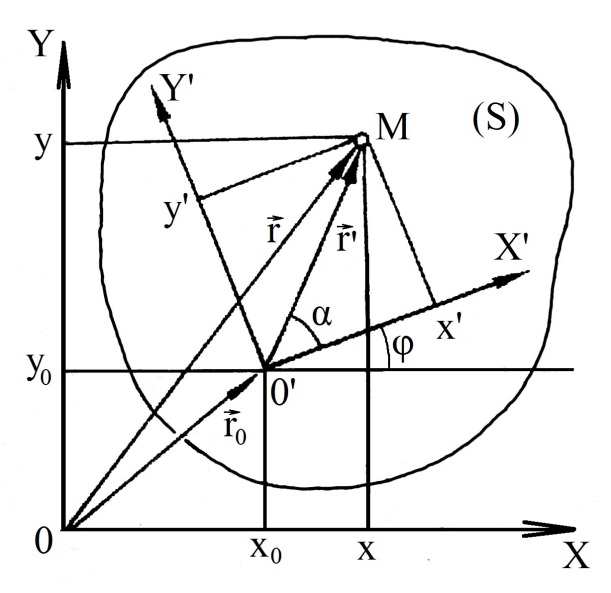 ехніці. Переважна більшість механізмів – це система твердих тіл, що здійснюють плоский рух. Прикладом плоского руху можуть бути рухи, що здійснюються в кривошипному механізмі . Розглянемо плоский рух детальніше. Для цього тіло, що здійснює плоский рух, уявно розділимо рядом паралельних площин так, щоб вектори швидкостей усіх точок тіла були паралельними утвореним площинам. Внаслідок такого поділу утвориться низка плоских фігур, накладених одна на одну.

Розглянемо рух однієї із отриманих фігур (S). Всі точки даної фігури рухаються з швидкостями, що лежать в площині фігури. Для визначення положення цієї фігури і траєкторії її точок виберемо

Рис. 4.1 дві системи координат, розташованих у площині фігури: одну систему XOY нерухому, а другу – X¹O¹Y¹, пов’язану з фігурою так , щоб у початковий момент часу осі обох систем відліку були паралельними. Вісь OZ в обох координатних системах напрямлена “ до нас”. Положення довільної точки M фігури (S) задається або радіус-вектором , проведеним із нерухомого початку, або радіус-вектором ,проведеним із початку O¹ рухомої системи відліку. Радіус-вектор початку рухомої системи координат позначимо через ₀. (Рис 4.1).

Із рисунка 4.1 видно що:

= + (4.1)

Якщо фігура (S) рухається, то радіс-векторз часом змінюється, а радіус-вектор r¹ залишається незмінним. Положення фігури (s) повністю визначається положенням рухомої системи координат відносно нерухомої. Для визначення положення рухомої системи відліку відносно нерухомої досить задати функції, які визначають залежність положення полюса O¹ від часу відносно положення початку координат O (f=r(t) ) і залежність від часу кута , який утворює вісь OX з віссю OX¹ . Кут в цьому випадку є кутом повороту радіус-вектора навколо полюса . Таким чином плоский рух твердого тіла повністю визначається рівнянням поступального руху полюса = (t) і рівнянням обертального руху = (t) навколо полюса.

Продиференціювавши за часом рівняння (4.1), отримаємо рівняння розподілу швидкостей у рухомій плоскій фігурі:

(4.2)

або

= (4.3)

де V₀ -швидкість поступального руху полюса, - лінійна швидкість обертального руху точки навколо полюса. Підставивши у (4.3) замість його знаення із формули (3.6) отримаємо:

= ₊ (4.4)

Отже , під час плоского руху швидкість довільної точки дорівнює векторній сумі швидкості

поступального руху тіла і лінійної швидкості яку б мала ця точка, якби полюс був нерухомий, а тіло оберталось би навколо нього з кутовою швидкістю .

Наприклад, якщо тіло здійснює плоский рух і деяка його точка А має швидкість

поступального руху (рис.4.2) то швидкість будь-якої точки B знаходимо як геометричну суму

_в = + , (4.5)

де V_AB –лінійна швидкість обертання точки B навколо точки A. V_AB напрямлена перпендикулярно до AB у напрямі обертання тіла.

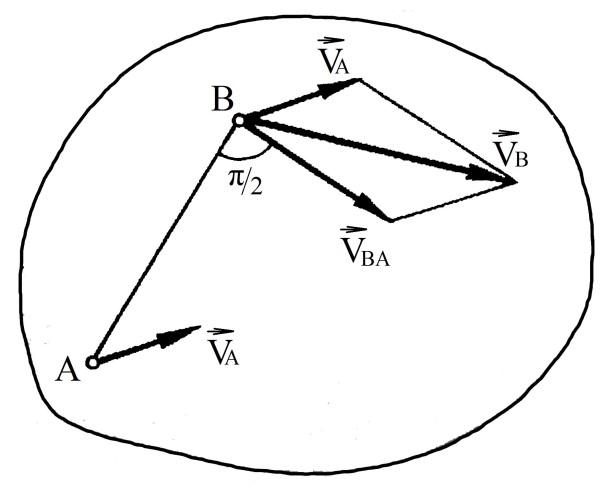
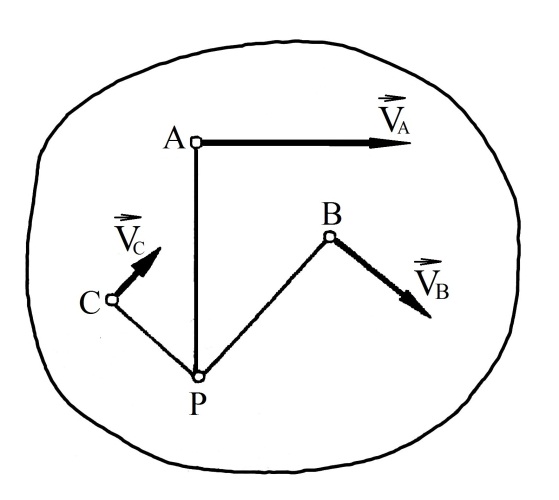
Рис. 4.2 Рис.4.3

Під час плоского руху тіла в кожний момент часу існує точка, швидкість якої у цей момент дорівнює нулю. Цю точку називають миттєвим центром швидкостей. Якщо прийняти миттєвий центр швидкостей за полюс, то закон розподілу швидкостей можна записати у вигляді:

=[ (4.6)

Таким чином, розподіл швидкостей у тілі, що здійснює плоский рух, у кожен момент часу такий, наче тіло обертається навколо нерухомої осі, що проходить через миттєвий центр ш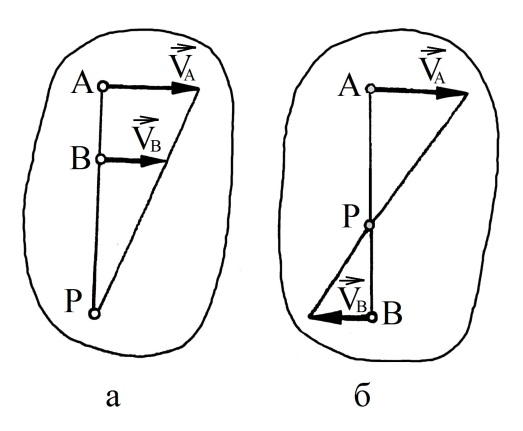 видкостей. Це означає що вектор швидкості довільної точки тіла, що здійснює плоский рух, перпендикулярний до радіус-вектора ,проведеного з миттєвого центра P у цю точку, а за модулем дорівнює добутку r (рис.4.3)

Якщо відомі швидкості двох довільних точок тіла, то положення миттєвого центру збігається хточкою перетину перпендикулярів,проведених із цих точок до напрямів швидкостей (рис. 4.3).

Рис. 4.4 У випадку,коли вектори швидкостей _A і _B лежать на паралельних прямих, а точки A і B лежать на перпендикулярі , проведеному до напрямів швидкостей ( рис 4.4а), то миттєвий центр обертання знаходиться у точці перетину перпендикуляра з прямою, проведеною через кінці векторів _A і _B. Якщо вектори швидкостей I лежать на паралельних прямих і мають протилежний напрям, а точки A і B лежать на перпендикулярі , проведеному до напрямів швидкостей, то миттєвий центр обертання знаходиться в точці перетину перпендикуляра з прямою, проведеною через кінці векторів _A і _B ( рис4.4б).

Розділ II Основи динаміки