Принцип відносності Галілея.
Для з’ясування питання про те, який вигляд матимуть закони механіки у рухомій системі відліку, з’ясуємо, як пов’язані між собою координати довільної точки М у рухомій та нерухомій системах відліку і отримаємо формули, які дають можливість перейти від координат даної точки в нерухомій системі відліку до її координат в рухомій системі відліку2.10)
Систему рівнянь ( 2 .10)
називають перетвореннями Галілея.
Рівняння t= t′ означає, що час у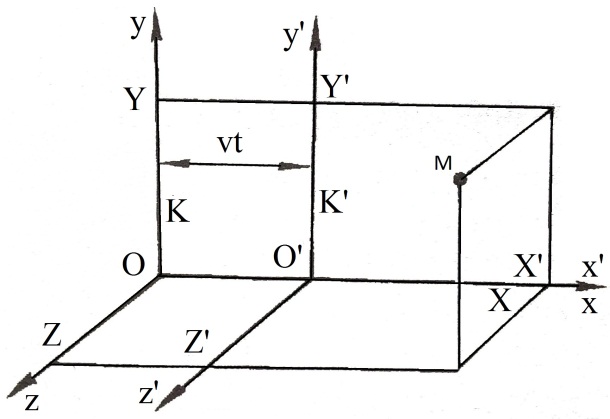
класичній механіці не залежить від
вибору системи відліку і протікає в
усіх інерціальних системах відліку
однаково.
Величини, що не змінюються внаслідок переходу від однієї системи відліку до іншої, називаються інваріантними. Отже, час є інваріантним відносно перетворень Галілея. Можна довести, що довжина стержня або відстань між двома точками твердого тіла однакова в обох
Рис. 2.1 системах відліку, тобто вони є інваріантними відносно перетворень Галілея.
( 2 .10)Зв’язок між складовими швидкостей точки М в обох системах відліку знаходимо диференціюванням системи рівнянь ( 2.1).
-
=
+
;
=
;
=
(2.11)
Рівняння ( 2 .11) у векторній формі записують у вигляді
-
(2.12)
Рівняння ( 2 .12) виражає
закон додавання швидкостей
я: швидкість матеріальної точки
відносно нерухомої системи відліку
дорівнює векторній сумі відносної
і переносної
швидкостей. Відносною швидкістю
називають швидкість руху матеріальної
точки відносно рухомої системи відліку,
а швидкість руху рухомої системи відліку
відносно нерухомої системи відліку
називається переносною швидкістю.
Швидкість руху матеріальної точки
відносно нерухомої системи відліку
називається абсолютною швидкістю.
Зв’язок між прискоренням точки відносно рухомої і нерухомої системи відліку, знаходимо диференціюванням рівняння ( 2 .12): у формулі 2.4 u замінити на v
-
або
(2.13)
Як видно із рівнянь ( 2 .13), прискорення є інваріантним відносно перетворень Галілея. З цього випливає, що всі системи відліку, які рухаються рівномірно і прямолінійно відносно інерційних системи відліку, будуть інерційними. Також під час переходу від однієї інерційної системи до іншої інерційної системи відліку сила як функція інваріантних величин не змінюється, тобто сила інваріантна відносно перетворень Галілея.
У рухомій системі
відліку другий закон запишеться у
вигляді:
=m∙
,
оскільки a = aʹ,
то другий закон Ньютона в рухомій
інерційній системі відліку матиме такий
самий вигляд, як у нерухомій системі
відліку:
= m
Таким чином, на основі сказаного вище можна сформулювати один з найважливіших принципів механіки – принцип Галілея: рівняння механіки Ньютона інваріантні відносно перетворень Галілея, тобто вони залишаються незмінними під час переходу від однієї інерційної системи до іншої.
Закони взаємодії і руху тіл в усіх інерційних системах відліку описуються одними і тими самими рівняннями, а це означає, що усі інерційні системи відліку рівноправні. Проте не варто думати, що характер руху в усіх інерційних системах відліку однаковий. Розглянемо приклад. Нехай на горизонтальній ділянці залізниці рівномірно рухається вагон. Нехай у вагоні вільно падає кулька без початкової швидкості відносно вагона. У системі відліку “вагон” ( у рухомій системі відліку) рух кульки буде прямолінійним. У системі відліку, пов’язаній із залізничними коліями (у нерухомій системі відліку), кулька матиме початкову швидкість, напрямлену горизонтально, що дорівнює швидкості руху вагона, а траєкторією руху буде парабола.
Принцип відносності Галілея охоплює механічні явища, що відбуваються в замкнених системах, а самі системи мають певні розміри і перебувають у незмінних зовнішніх умовах.
Тому можна дати ще й таке еквівалентне формулювання принципу відносності Галілея: ніякими механічними дослідами, проведеними всередині інерційної системи відліку, неможливо встановити: система перебуває у стані спокою чи рухається прямолінійно і рівномірно.
Пізніше принцип відносності Галілея був поширений на всі фізичні явища, тому його можна сформулювати так: ніякими фізичними дослідами, проведеними всередині інерційної системи відліку, неможливо встановити: система перебуває в стані спокою чи рухається прямолінійно і рівномірно.