§22. Закон збереження моменту імпульсу.

Якщо сумарний момент сил, які діють на тіло або систему тіл, дорівнює нулю (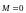 ), то із формули Error: Reference source not found випливає, що або

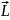= ∙I ( 22.1)

Таким чином, якщо сума моментів зовнішніх сил дорівнює нулю, то момент імпульсу системи не змінюється з часом. У цьому полягає закон збереження моменту імпульсу.

Якщо момент інерції тіла, яке обертається, змінюється, а момент прикладених сил залишається сталим, то кутова швидкість тіла буде змінюватися. Це можна продемонструвати за допомогою платформи, яка обертається навколо вертикальної осі (лава Жуковського). Людина з гантелями в руках знаходиться на лаві, яка обертається з кутовою швидкістю w₁ (Рис.22.18).

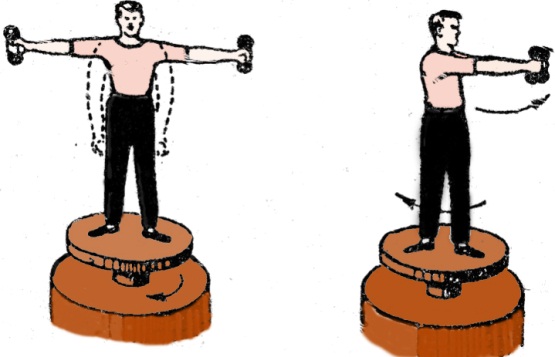
Рис.22.18

Нехай момент інерції людини і лави дорівнює І₁. Коли людина наблизить руки до осі обертання, то момент інерції зменшиться до І₂, а це приведе до збільшення швидкості обертання до w₂, бо, згідно із Error: Reference source not found, виконуватиметься рівність: . Фігурист на ковзанах, що виконує пірует, може змінювати швидкість свого обертання, змінюючи положення рук і ніг. Цим прийомом користуються спортсмени під час стрибків у воду та виконання акробатичних вправ, пов’язаних із обертанням у повітрі (Рис.22.19). Під час стрибків у воду спортсмен, стрибнувши, складається в «клубочок», його момент інерції зменшується і він починає швидко обертатись. Зробивши декілька обертів, він розпрямляється, момент його інерції зростає, а швидкість обертання зменшується.

У наведених прикладах момент сили тяжіння дорівнює нулю, бо вона прикладена до центра мас, через який проходить вільна вісь обертання, а отже, зберігається момент кількості руху. Змінюючи момент інерції тіла, людина змінює кутову швидкість обертання.

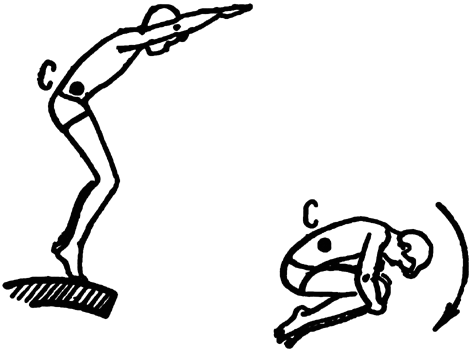
Рис.22.19

Закони збереження імпульсу, моменту імпульсу та енергії відіграють важливу роль у природі та науці. Вони виконуються як в макро-, так і в мікросвіті. Їх можна застосувати як до звичайних тіл, так і до мікрочастинок, а також до тіл космічних розмірів. У природі відсутні явища, в яких би не виконувався будь-який із законів збереження. Необхідно підкреслити, що закони збереження є універсальними законами природи і виконуються завжди.

§23. Кінетична енергія обертального руху. Аналогія понять та рівнянь при поступальних і обертальних рухах

Кінетична енергія тіла, яке обертається, дорівнює сумі кінетичних енергій усіх частинок, з яких воно складається:

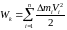. ( 23.1)

Оскільки = , то формулу ( 23.1) можна записати у вигляді:

(23.2)

де І – момент інерції тіла відносно осі обертання, L – момент кількості руху, w - кутова швидкість.

Якщо тіло масою m бере участь у поступальному і обертальному русі одночасно (наприклад, колесо, яке котиться), то його кінетична енергія дорівнює сумі кінетичних енергій поступального та обертального рухів:

(23.3)

де V – швидкість руху центра мас, w та І – кутова швидкість та момент інерції тіла відносно осі обертання, яка проходить через центр мас.

На завершення відзначимо корисну аналогію між величинами і рівняннями, які описують поступальний і обертальний рухи (табл. 2)

Таблиця 2

Поступальний рух	Обертальний рух
1. Лінійна швидкість,	1. Кутова швидкість,
2. Лінійне прискорення,	2. Кутове прискорення,
3. Сила,	3. Момент сили,
4. Маса, m	4. Момент інерції, I
5. Імпульс, = m	5. Момент імпульсу, = I
6. Основний закон динаміки: , або	6. Основне рівняння динаміки обертального руху: , або
7. Кінетична енергія: W =	7. Кінетична енергія обертального руху: