2. Векторна величина , яка дорівнює добутку моменту інерції на кутову швидкість, називається моментом імпульсу:

(21.90)

Напрям і 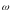співпадають. Модуль моменту імпульсу матеріальної точки масою m, яка рухається по колу радіуса r, виражається формулою:

,

де w - кутова швидкість точки, – лінійна швидкість точки (Error: Reference source not found)П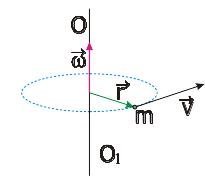 ідставивши в Error: Reference source not found замість його значення і вважаючи, що момент інерції твердого тіла є величина стала ( I=const ), одержимо:

Рівняння Error: Reference source not found називають основним рівнянням динаміки обертального руху. Із рівняння Error: Reference source not found видно, що швидкість зміни моменту імпульсу тіла, яке обертається, дорівнює сумі моментів сил, які діють на це тіло.

Рис. 21.3

Із формули Error: Reference source not found видно, що момент інерції І характеризує інертні властивості тіл під час обертального руху, тобто момент інерції відіграє таку ж роль, що й маса під час поступального руху. Момент інерції – скалярна величина, яка залежить від маси тіла та її розподілу в тілі відносно осі обертання. Одиницею вимірювання моменту інерції в системі СІ є 1кГм². Обчислюють момент інерції за формулою:

(21.91)

де r – густина речовини, V – об’єм тіла.

Обчислення моменту інерції тіл – задача дуже складна. Вона легко розв’язується, якщо тіло однорідне і має просту геометричну форму. Момент інерції тіл складної форми з нерівномірним розподілом мас момент інерції визначають експериментальним шляхом. Формули, за якими можна обчислити момент інерції деяких простих тіл, подано в таблиці 1.

Гюйгенса-Штейнера можна знайти момент інерції цього ж тіла відносно осі О₁О_1, паралельної даній Якщо відомо момент інерції відносно осі ОО, яка проходить через центр мас, то за теоремою осі ОО: , де d – віддаль між осями, m – маса тіла (Error: Reference source not found.4).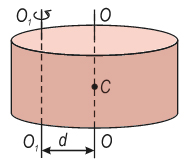

Теорема Гюгенца-Штейнера.

Момент інерції твердого тіла відносно довільної осі О₁О₁ дорівнює сумі моментів інерції відносно осі ОО, що проходить через центр мас паралельно даній осі та добутку маси тіла на квадрат відстані між осями (Error: Reference source not found)

I = 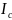+ md

Рис. 214

3. Вільні осі обертання

В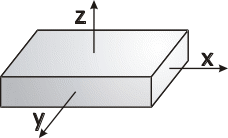 ісь обертання, яка зберігає своє положення в просторі за відсутності зовнішніх дій, називається вільною віссю. Розрахунки та експерименти показують, що вільні осі завжди проходять через центр мас тіла, а обертання буде стійким лише відносно тих осей, момент інерції тіла відносно яких або максимальний, або мінімальний.

Рис.22.17

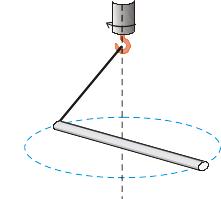
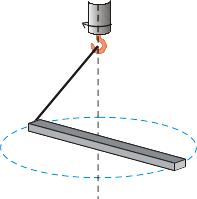
Рис.21.5 Рис . 21.6

Н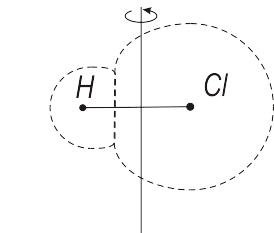 априклад, у паралелепіпеда (Рис.22.17) стійкими будуть осі ХХ та ZZ. Вільне (стійке) обертання може відбуватися тільки відносно однієї із цих осей. Наприклад, стержень чи брусок підвішений на нитці, яку приводять в обертальний рух, також починають обертатись відносно стійкої вільної осі (Рис.21.).

Вільне обертання молекул також відбувається відносно стійких (вільних) осей. На Error: Reference source not foundтака вісь показана для хлористого водню (HCl).

Рис. 21.7

Таблиця 1

Тіло	Положення осі	Момент інерції І
Порожнистий циліндр (обруч) радіуса R і масою m	В ісь циліндра (обруча) проходить через центр мас перпендикулярно до площини, у якій лежить обруч.
Суцільний циліндр (диск) масою m і радіуса R	В ісь циліндра (диска) проходить через його центр перпендикулярно до площини диска.
Суцільний диск масою m і радіуса R	В ісь лежить в площині диска і проходить через його центр.
Куля радіуса R і масою m	В ісь проходить через центр кулі
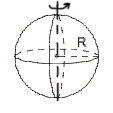
Тонкостінна сфера радіуса R і масою m	Вісь проходить через центр сфери
Прямий тонкий стержень довжиною l і масою m	В ісь перпендикулярна до стержня і проходить через його середину
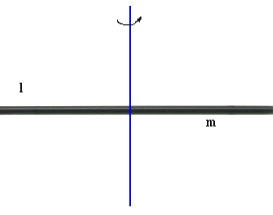
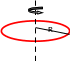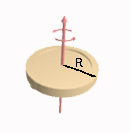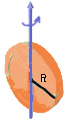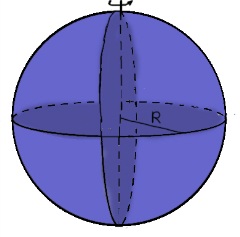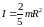
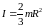
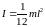
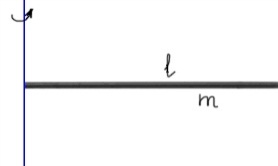Той же стержень	В ісь перпендикулярна до стержня і проходить через його край