§21. Основне рівняння динаміки обертального руху. Момент інерції. Момент імпульсу (момент кількості руху)

1. Обертальним рухом називають такий рух твердого тіла, під час якого всі його точки рухаються по колах, центри яких лежать на одній прямій, що називається віссю обертання.

Кутова і лінійна швидкість точок тіла, що лежать на осі обертання, дорівнює нулю. Для вивчення законів обертання твердого тіла користуються поняттями моменту сили та моменту інерції. Моментом сили відносно осі називають добуток сили на плече

М = Fd,

де d – плече сили. Плечем сили називають найкоротшу віддаль від осі обертання до напрямку дії сили. Для кращого розуміння цих понять розглянемо рух однієї матеріальної точки А масою m по колу радіуса r. Нехай на точку діє стала за величиною сила . Розкладемо цю силу на складові: – тангенціальну складову, напрямлену вздовж дотичної до кола, і – нормальну складову, напрямлену вздовж радіуса (Рис.21.16).

Під дією тангенціальної складової сили матеріальна точка набуває тангенціального прискорення, яке можна визначити, застосувавши другий закон Ньютона:

m (21.1)

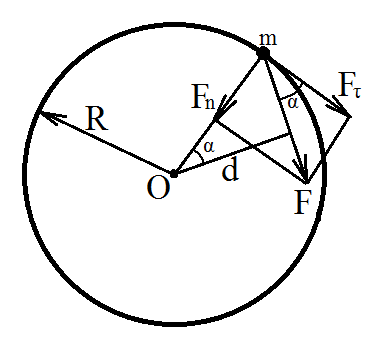
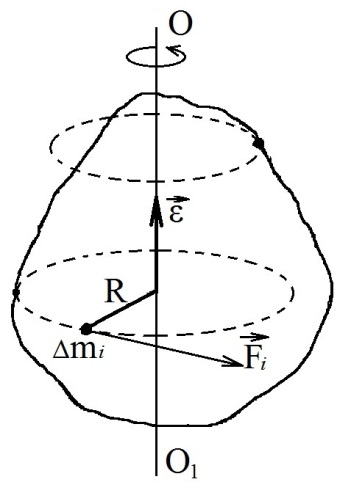
Рис.21.16 Рис. 21.2

Як видно з рис. 21.1, де – кут між вектором сили та дотичною до кола, проведеній в точці прикладання сили _. Тангенціальне прискорення пов’язане із кутовим співвідношенням: , де – кутове прискорення,. Підставивши у формулу Error: Reference source not found замість та їх значення, отримаємо:

(21.83)

Помноживши ліву та праву частини рівняння (21.83) на r, отримаємо:

(21.84)

Добуток дорівнює довжині перпендикуляра, опущеного із точки О на напрям дії сили, тобто є плечем сили F (rcos ). Величина , що чисельно дорівнює добутку величини сили на плече є моментом сили відносно осі О. Величина чисельно дорівнює добутку маси m матеріальної точки А на квадрат її віддалі від осіО (центру обертання) і називається моментом інерції І точки А відносно осі ( вісь О перпендикулярна до площини рисунка). Ввівши момент сили М та момент інерції І, рівняння (21.84) запишемо у вигляді:

(21.85)

Нехай у нас є тіло, що обертається навколо осі ОО₁. Уявно розділимо це тіло на п елементарних частинок, таких малих, щоб кожну з них можна було вважати матеріальною точкою. Кожна із цих точок які знаходяться на віддалі від осі обертання, рухається із однаковою кутовою швидкістю і однаковим кутовим прискоренням, але різними лінійними швидкостями і різними тангенціальними прискореннями.

Кожна точка (і – номер матеріальної точки) під дією сили рухаючись по колу радіуса r_i, набуває тангенціального прискорення Згідно з другим законом Ньютона сила дорівнює:

=

Помноживши ліву та праву частину цього рівняння на і врахувавши те, що одержимо:

(21.86)

Врахувавши те, що , рівняння (21.86) можна записати у вигляді:

(21.87)

або у векторній формі:

(21.88)

Вектори і мають однаковий напрям. Добуток називається моментом інерції матеріальної точки відносно осі обертання.

Записавши рівняння (21.7) для всіх n точок, з яких складається тіло, і почленно їх додавши, одержимо:

(21.89)

Позначимо : = ; (21.9)

I = (21.10

Рівняння (21.9) визначає суму моментів сил, прикладених до тіла, а рівняння (21.10) – суму моментів інерції всіх матеріальних точок, з яких складається тіло ( момент інерції тіла відносно осі обертання).

Моментом інерції тіла відносно осі називають суму моментів інерції всіх його матеріальних точок відносно цієї ж осі. Враховуючи ці позначення, рівняння (21.85) можна записати у вигляді:

= I або = (21.9)

Формула Error: Reference source not found виражає основне рівняння динаміки обертального руху твердих тіл (другий закон Ньютона для обертального руху).

Кутове прискорення тіла, що обертається, прямо пропорційне сумі всіх прикладених до тіла моментів сил і обернено пропорційне моменту інерції тіла відносно осі обертання.