§20. Абсолютно пружний і абсолютно непружний удар

Ударом називають сукупність явищ, що виникають під час короткочасної взаємодії тіл під час їх зіткнення. Під час удару тіла деформуються і в них виникають досить великі сили пружності і сили тертя, також виникають коливання і хвилі. Процес удару поділяють на два періоди. У першому періоді під час зіткнення відбувається деформація тіл і виникають сили пружності, які гальмують рух, а кінетична енергія тіл перетворюється в потенціальну енергію деформації. Під час другого періоду всі процеси відбуваються у зворотному напрямку і частина потенціальної енергії деформації, якщо удар непружний, перетворюється в кінетичну енергію руху тіл, а інша частина – у внутрішню енергію. Процеси, що відбуваються під час удару тіл, залежать від їх природи, розмірів, форми, швидкості відносного руху тощо. Удари поділяють на абсолютно пружні, абсолютно непружні і пружно-пластичні.

Абсолютно пружним називають такий удар, після якого в тілах, що зазнали зіткнення, не залишається жодних деформацій, а механічна енергія тіл після зіткнення дорівнює механічній енергії до зіткнення. Абсолютно непружним називають такий удар, після якого деформації, зумовлені зіткненням тіл, повністю зберігаються, а тіла після зіткнення рухаються як одне ціле.

Близькими до абсолютно пружного удару є зіткнення куль, виготовлених із слонової кості та куль, виготовлених із високоякісної сталі. Прикладом абсолютно непружного удару є зіткнення пластилінових куль, захоплення електрона позитивним іоном та ін.

Пружно-пластичний удар займає проміжне положення між абсолютно пружним і абсолютно непружним ударом. Під час пружно-пластичного удару частина кінетичної енергії перетворюється у внутрішню.

В наслідок того, що під час удару тіл виникають досить великі сили, дією інших сил, що постійно діють на дані тіла (наприклад силою тяжіння), можна знехтувати.

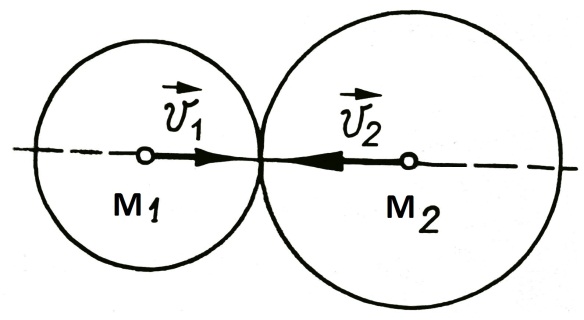
Рис.20.14

Рис.20.15

Спільну нормаль, проведену до поверхонь у точці дотику під час удару, називають лінією удару (Рис.20.14 штрихова лінія). Удар називають центральним, якщо лінія удару проходить через центри мас тіл, що стискаються (Рис.20.15), а напрями швидкостей тіл до зіткнення збігаються з лінією удару.

Взаємодія тіл під час удару відбувається за дуже короткі проміжки часу, тому під час удару можуть розвиватись досить великі потужності.

Нехай дві кулі масами m₁ та m₂ відповідно, рухаючись зі швидкостями та , здійснюють абсолютно пружний центральний удар. Нехай швидкості куль після удару відповідно дорівнюють та . Виберемо систему відліку так, щоб напрям осі OX збігався з напрямом вектора швидкості V₁. Оскільки удар центральний, то у вибраній системі відліку проекції векторів швидкості на вісь OY дорівнюють нулю, тому ми будемо розглядати проекції векторів лише на вісь OX.

Оскільки дією всіх інших сил (крім сили пружності, що виникає під час удару) можна знехтувати, то кулі становлять замкнену систему. У замкненій системі виконується закон збереження імпульсу і кінетичної енергії:

(20.75)

Систему рівнянь (20.75) можна записати у вигляді:

.

(20.76)

Розв’язавши систему рівнянь (20.76), знайдемо швидкості куль після взаємодії U₁ та U₂:

;	(20.77)
,	(20.78)

У формулах (20.77) і (20.78) знаки швидкостей V₁ та V₂ беруть із знаком плюс, якщо їх напрям збігається із додатнім напрямом осі OX, якщо ж швидкості мають протилежний напрям, то їх необхідно брати зі знаком мінус. Якщо при розв’язанні задачі отримані швидкості U₁ та U₂ додатні, то їх напрям збігається із напрямом осі OX, якщо ж від’ємні, то їх напрям протилежний додатному напрямку осі ОХ.

Розглянемо часткові випадки.

1. Маси куль однакові (m₁=m₂). Із рівнянь (20.77) і (20.78) видно, що в цьому випадку U₁=V₁ і U₂=V₂. Це означає, що кулі однакових мас обмінюються швидкостями.

Якщо друга куля в початковий момент часу була нерухома V₂ = 0, то формули (20.77) і (20.78) набувають вигляду:

; (20.5)

Із Error: Reference source not found видно, що рух куль після взаємодії залежить від співвідношення мас куль. Якщо маси куль однакові (m₁=m₂), то після удару перша куля зупиняється, а друга куля рухається зі швидкістю першої кулі (U₂=V₁) у напрямку руху першої кулі.

Якщо маса першої кулі більша, ніж маса другої кулі (m₁>m₂), то перша куля продовжує рухатись у тому самому напрямі, але з меншою швидкістю (U₁<V₁), а друга куля після удару рухається зі швидкістю U₂, більшою за початкову швидкість першої кулі (U₂>V₁).

Якщо маса першої кулі менша, ніж маса другої кулі (m₁<m₂), то перша куля після удару змінює напрям свого руху на протилежний, але з меншою швидкістю, а друга куля рухається у тому напрямі, у якому рухалась перша куля до удару.

Якщо маса першої кулі набагато менша, ніж маса другої кулі (m₁<<m₂), то U₁=-V₁ – перша куля після удару рухається у протилежному напрямі, а друга куля залишається нерухомою (U₂ 0).

2. Під час абсолютно непружного удару обидві кулі об’єднуються і рухаються як одне ціле з швидкістю U (наприклад, кулі виготовлені з глини). В цьому випадку виконується закон збереження імпульсу, який для випадку центрального удару запишемо у вигляді:

,

звідки визначимо U:

U=

(20.79)

Під час непружного удару частина кінетичної енергії куль перетворюється у внутрішню енергію, втрата кінетичної енергії дорівнює роботі, виконаній неконсервативними силами під час непружної деформації куль, і дорівнює зміні енергії куль:

А =

(20.80)

Підставивши у (20.80) замість U його значення (20.79) після нескладних математичних перетворень, отримаємо:

А =

(20.81)

Як видно із формули (20.81), робота, виконана під час непружної деформації, пропорційна квадрату відносної швидкості (V₁ – V₂) руху тіл.

Якщо друге тіло нерухоме (V₂=0), то рівняння (20.81) набуде вигляду:

А = .

(20.82)

Ситуація, під час якої одне тіло залишається нерухомим, а інше рухається, спостерігається під час кування металу, дроблення крихких тіл та ін. У цьому випадку корисно якнайбільшу частину кінетичної енергії рухомого тіла перетворити у роботу деформації. Як видно із формули (20.82), для збільшення частини енергії, що перетворюється у роботу деформації, необхідно збільшити масу нерухомого тіла m₂.

Якщо удар використовують для переміщення нерухомого тіла з метою подолання опору (забивання цвяхів, вбивання паль в землю і ін.), то необхідно зменшити частину енергії, яка перетворюється в роботу деформації і максимально зберегти кінетичну енергію обох тіл після удару. Для цього необхідно зменшити масу нерухомого тіла (наприклад, цвяха) і збільшити масу рухомого тіла (наприклад, молотка).

РОЗДІЛ Y. Основи динаміки обертального руху