§14. Межі застосування законів класичної механіки
Закони Ньютона в елементарній формі запису добре описують рух макроскопічних тіл, швидкість яких мала порівняно з швидкістю світла. Але ці закони непридатні для описування руху об’єктів мікросвіту (атомів, молекул і т.п.) та тіл, які рухаються з швидкостями, близькими до швидкості світла. На основі розвитку теорії атома виник новий розділ фізики – квантова механіка, де було введено принципово нові поняття, відсутні в механіці Ньютона.
Механіку Ньютона не можна застосовувати до руху бистрих (релятивістських) частинок, швидкість яких наближається до швидкості світла. Рух таких частинок описується законами релятивістської механіки, розробленої на основі спеціальної теорії відносності. Згідно з цією механікою, у жодній системі відліку тіло не може набути швидкості, більшої за швидкість світла у вакуумі. Згідно з спеціальною теорією відносності, маси рухомих частинок, проміжки часу між подіями, довжини відрізків залежать від швидкості руху тіл в даній системі відліку. Наприклад, маса рухомого тіла визначається за формулою:
,
де
– маса нерухомого тіла (маса спокою), m
– маса того ж тіла, яке рухається в даній
системі відліку з швидкістю V,
c ‑ швидкість
поширення світла в вакуумі. Якщо V<<c,
то рівняння релятивістської і класичної
фізики співпадають, а це означає, що
механіка Ньютона є частковим випадком
релятивістської механіки. Розвитком
науки ньютонівська механіка не була
перекреслена, а було встановлено межі
її застосування.
Отже, закони механіки, розглянуті вище, можна застосовувати лише до макросвіту у випадку, коли швидкість руху набагато менша за швидкість світла у вакуумі.
Розділ IY. Механічна робота. Механічна енергія. Закон збереження механічної енергії.
§ 15. Механічна робота. Потужність
1. Механічна робота.
Механічною
роботою постійної сили
на прямолінійній ділянці шляху S
називають фізичну величину, яка чисельно
дорівнює добутку модуля переміщення S
та проекції сили
на напрям переміщення:
-
(15.59)
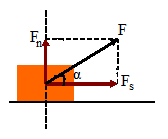
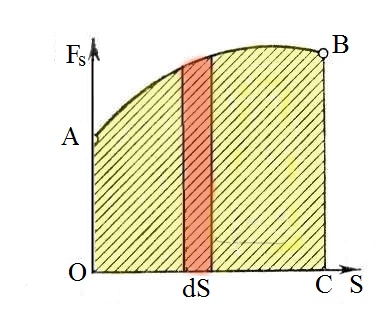
Рис. 15.1 Рис.15. 2
Як видно із
Error: Reference source not found,
,
тому формулу (15.59) можна записати у
вигляді:
-
,(15.60)
де
– кут між напрямком переміщення і
напрямом дії сили. Як видно із (15.2), робота
може бути як додатною (якщо
),
так і від’ємною (якщо
).
Якщо
,
то робота не виконується (А=0).
Одиницею
роботи в системі СІ є джоуль (Дж): Робота
1 Дж – це робота, .яку виконує сила в один
ньютон під час переміщення точки її
прикладання на один метр за умови, що
кут між напрямком дії сили і напрямком
переміщення дорівнює нулю (
):
1 Дж=1 Н·м
Розглянемо випадок, коли рух відбувається по криволінійній траєкторії під дією змінної сили (Error: Reference source not found).
Для обчислення
роботи траєкторію уявно ділять на
елементарні ділянки
,
такі малі, щоб кожну з них можна було
вважати прямолінійною, а діючу силу на
цій ділянці – сталою величиною. Тоді
елементарна робота dA,
яку виконує сила F на
елементарній ділянці dS,
може бути обчислена за формулою (15.59):
-
.(15.61)
Обчисливши роботу на кожній елементарній ділянці, обчислюють загальну роботу як суму елементарних робіт:
-
.(15.62)
Роботу
можна зобразити графічно. Відкладемо
по осі абсцис довжину пройденого шляху
S, а по осі ординат –
значення складової сили
(Error: Reference source not found).
Нехай
крива АВ зображає значення сили
у різних точках шляху для певного
довільного вибраного випадку. Уявно
розділимо пройдений шлях на елементарні
відрізки
,
такі малі, щоб діючу силу
на цій ділянці шляху можна було вважати
сталою. Елементарна робота
,
виконана на цій ділянці
,
дорівнює добутку сили
на величину переміщення
і зобразиться площею елементарної
криволінійної трапеції помаранчевого
кольору на Error: Reference source not found. Вся робота
на шляху S дорівнює сумі
елементарних робіт і графічно зобразиться
площею заштрихованої фігури ОАВС.