Розділ III. Неінерційні системи відліку. Сили інерції.

§11.Неінерційні системи відліку, що рухаються поступально. Невагомість. Принцип еквівалентності

1. Неінерційною називають систему відліку, яка рухається з прискоренням відносно інерційної.

Найпоширенішими неінерційними системами відліку є системи, що рухаються з малими швидкостями прямолінійно з прискоренням відносно інерційних систем відліку. В таких системах відліку справедливі перетворення Галілея.

Закони Ньютона та інші закони динаміки виконуються лише в інерційних системах відліку. В неінерційних системах відліку ці закони не виконуються. Розглянемо приклад. Нехай на гладенькій платформі, що рухається рівномірно і прямолінійно, лежить куля масою m. На цій самій платформі знаходиться спостерігач. Нехай у певній точці на поверхні землі, повз яку проходить платформа, знаходиться інший спостерігач. Обидва спостерігачі спостерігають за кулею. На кулю діє сила земного тяжіння mg і сила реакції опори N (Рис.11.8а), ці сили зрівноважують одна одну (mg=N), і в рухомій системі відліку, пов’язаній з платформою, куля перебуває в стані спокою, а в нерухомій системі відліку (Земля) куля рухається рівномірно і прямолінійно з швидкістю, що дорівнює швидкості руху платформи відносно нерухомої Землі.

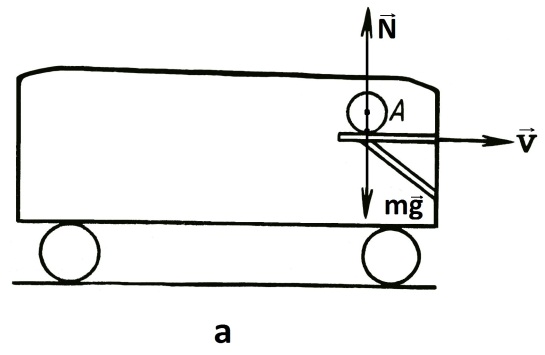
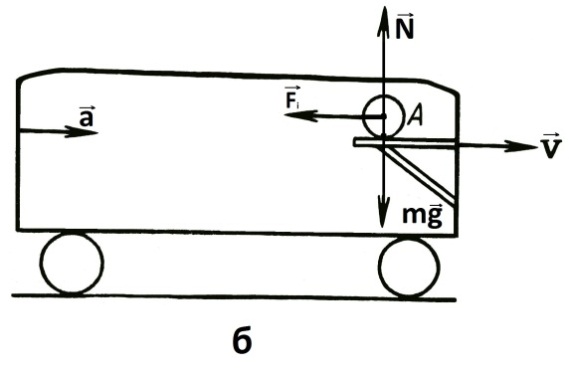
Рис.11.8

Нехай в момент, коли платформа проходить повз спостерігача, пов’язаного із Землею (нерухомою системою відліку), вона починає рухатись із прискоренням . В цьому випадку система відліку, пов’язана з платформою, стане неінерційною, і спостерігач, що знаходиться на платформі, виявить, що куля почала рухатись відносно платформи з прискоренням а, рівним за величиною і протилежним за напрямом прискоренню, якого набула платформа (Рис.11.8б). В системі відліку, пов’язаній із платформою, як і раніше сила тяжіння, прикладена до кулі, урівноважується силою реакції опори, і рівнодійна цих сил дорівнює нулю, але куля рухається з прискоренням. Таким чином, в неінерційній системі відліку не виконуються закони Ньютона.

Спостерігач, що знаходиться в інерційній системі відліку (пов’язаній з поверхнею Землі) виявить, що куля продовжує рухатись рівномірно і прямолінійно у відповідності з Законами Ньютона, а вагон (рухома система відліку) змінює свою швидкість.

Для того, щоб в неінерційних системах відліку можна було застосувати закони Ньютона вводять особливі сили – сили інерції. В неінерційних системах відліку, окрім звичайних сил, що виникають внаслідок взаємодії тіл, діють ще сили інерції F_і. Сили інерції – це реальні сили, тому, що завжди можна вказати наслідки їхньої дії. Позначивши аʹ – прискорення тіла відносно неінерційної системи відліку, другий закон Ньютона в неінерційній системі відліку запишемо у вигляді:

m

(11.45)

де m – маса тіла, – рівнодійна сил, що діють на тіло з боку інших тіл в інерційній системі відліку. Під дією цих сил тіло рухається з прискоренням а₀. Врахувавши сказане, формулу (11.45) запишемо у вигляді:

m

(11.46)

Визначивши із формули (11.46), отримаємо:

(11.47)

Отже, сила інерції чисельно дорівнює масі тіла, помноженій на різницю прискорення тіла відносно рухомої і нерухомої системи відліку.

Для з’ясування питання про напрям сили інерції розглянемо декілька випадків.

2. Неінерційні системи відліку, що рухаються поступально.

Нехай неінерційна система відліку рухається прямолінійно з прискоренням а₀ відносно інерційної. Нехай матеріальна точка рухається з прискоренням аʹ відносно рухомої системи відліку. Прискорення точки відносно нерухомої системи відліку дорівнює векторній сумі прискорення відносно рухомої системи відліку і прискорення рухомої системи відліку відносно нерухомої:

(11.48)

Із формули (11.48) визначимо аʹ ( = ) і підставимо його значення у формулу (11.3):

(11.49)

Знак мінус у формулі (11.49) означає, що сила інерції F_i і прискорення а₀ мають протилежний напрям.

Отже, у неінерційних системах відліку, що рухаються поступально, сила інерції напрямлена протилежно до напряму прискорення неінерційної системи відліку і дорівнює добутку прискорення неінерційної системи відліку на масу тіла.

Рис.11.9

Д ля ілюстрації сказаного вище розглянемо приклад. На візочку, що рухається поступально з прискоренням а, на нитці закріплена кулька (Рис.11.9). В системі відліку “візок” кулька перебуває в стані спокою під дією трьох сил: сили Т натягу нитки, сили інерції F_i та сили mg – земного тяжіння.

Запишемо рівняння кульки в неінерціальній системі відліку:

(11.50)

m , за умовою задачі =0, тому рівняння набуде вигляду:

Розв’язавши рівняння Error: Reference source not found, отримаємо значення тангенса кута φ, на який вона відхилиться від вертикалі: tgφ =

3 Невагомість. Принцип еквівалентності.

Вагою називають силу, з якою тіло діє на опору або підвіс.

Н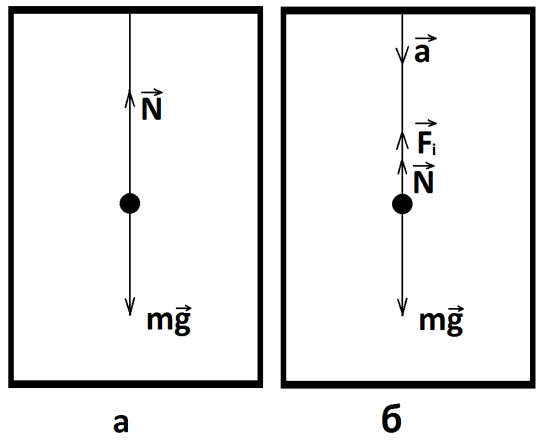 ехай тіло масою m, підвішене на пружинці, знаходиться в системі відліку, що починає рухатись з прискоренням а, напрямленим вертикально вниз. У початковий момент часу, коли система відліку нерухома, на тіло діє сила N пружності пружини і сила тяжіння mg. Під дією цих сил тіло знаходиться в стані спокою (Рис.11.10а). Запишемо другий закон Ньютона для цього випадку: mg – F_пр = 0 => F_пр = mg.

Отже, якщо підвіс нерухомий і система відліку інерційна, то вага тіла дорівнює силі тяжіння.

У випадку, коли система відліку рухається з прискоренням а, напрямленим вертикально вниз, на тіло діє сила інерції F_і, напрямлена вертикально вгору, сила тяжіння mg та сила пружності N (Рис.11.10б). Під дією цих сил тіло знаходиться в стані спокою. В цьому випадку рівняння руху записуємо у вигляді mg-F_i-F_пр=0, або

mg – ma – F_пр = 0 (11.7)

Рис.11.10 З рівняння Error: Reference source not found визначаємо силу пружності, яка чисельно дорівнює вазі тіла.

Fпр = mg – ma, або Fпр =m(g –а)

(11.51)

Із рівнянь(11.51) видно, що коли система відліку опускається вниз з прискоренням а, то вага тіла зменшується. Якщо прискорення руху рухомої системи відліку дорівнює прискоренню вільного падіння (a=g), то вага тіла дорівнює нулю. В цьому випадку говорять, що тіло перебуває в стані невагомості.

Отже, у системі відліку, яка вільно падає, сили інерції повністю компенсують дію сили тяжіння, внаслідок чого рух відбувається так, начебто немає ні сил тяжіння, ні сил інерції.

Системи відліку, які вільно падають, використовують для отримання стану невагомості в земних умовах.

Якщо система відліку рухається прямолінійно з прискоренням відносно інерційної системи відліку, то всі явища, що відбуваються в цій системі відліку протікають так, ніби з’явилось додаткове поле тяжіння, прискорення вільного падіння якого дорівнює прискоренню, з яким рухається система відліку. Це твердження називається принципом еквівалентності. Принцип еквівалентності можна сформулювати ще й так: в системі відліку наявність її прискорення не відрізняється від присутності відповідного поля тяжіння.

Конкретне поле тяжіння змінюється від точки до точки і в різних точках простору набуває різних значень. Це означає, що неможливо підібрати систему відліку, яка рухається так, що її прискорення в кожній точці простору еквівалентне за своєю дією з полем тяжіння, що діє в даній системі відліку.

Якщо розглядати поле тяжіння в малій області простору (наприклад, біля поверхні Землі), то можна вважати його однорідним, тому в цій області можна застосувати принцип еквівалентності і робити висновки про перебіг фізичних процесів.