1. 2. Вага тіл.

Силу тяжіння не можна ототожнювати з вагою тіла.

Вагою називають силу, з якою тіло діє на горизонтальну опору або підвіс. На вагу тіла впливає характер руху системи відліку.

Якщо опора знаходиться в стані спокою або рухається рівномірно і прямолінійно, то вага тіла за величиною дорівнює силі тяжіння . Якщо опора рухається з прискоренням , напрям якого збігається з напрямом сили тяжіння, то вага тіла зменшується і визначається за формулою:

P=m(g-a),

(7.26)

якщо = , то наступає стан невагомості і P=0. У цьому випадку тіло не тисне на опору і усі явища в цій системі відліку протікають так, ніби зникло земне тяжіння. Якщо ж напрям прискорення опори протилежний напряму дії сили тяжіння, то вага зростає і її визначають за формулою:

P=m(g+a).

(7.27)

У цьому випадку вага зростає і в даній системі відліку всі явища протікають так, неначе зросла сила земного тяжіння. Таке явище називають перевантаженням.

Перебування живих організмів у невагомості призводить до порушення звичайного для них режиму життєдіяльності, і протікання біологічних процесів змінюється. Перевантаження живих організмів також призводить до зміни протікання багатьох біологічних процесів. Багатократне перевантаження може бути смертельно небезпечне для людини.

§8. Космічні швидкості

Космічною швидкістю називають швидкість, яку необхідно надати тілу, щоб воно стало штучним супутником планети чи зорі або вийшло із сфери дії сил притягання зорі і рухалось би навколо центра Галактики як штучна “зоря”.

Першою космічною швидкістю називають швидкість, яку необхідно надати тілу в горизонтальному напрямі, щоб воно рухалось по коловій орбіті навколо планети, тобто стало її штучним супутником.

Нехай тіло рухається по коловій орбіті навколо планети радіуса R і масою m на висоті h над її поверхнею (Рис.8.7). На тіло діє сила всесвітнього тяжіння та сила інерції

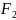
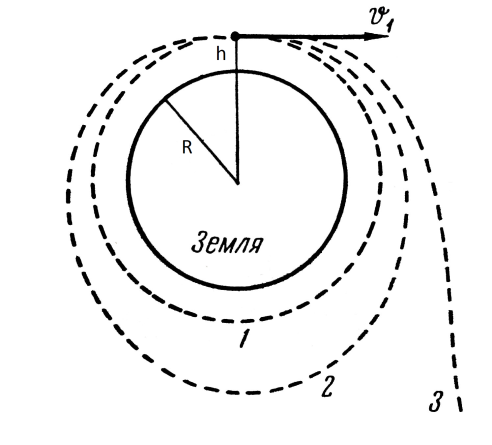
= G	(8.28)
=	(8.29)

Для того щоб тіло рухалось по коловій орбіті, не падаючи на поверхню планети, необхідно, щоб сила врівноважувалась силою _:

Рис.8.7

F1 = F2

(8.30)

Підставивши у формулу Error: Reference source not found замість і їх значення із Error: Reference source not found і Error: Reference source not found, отримаємо:

G =

(\8.31)

Після відповідних скорочень формула (\8.31) набуде вигляду:

G =

(8.32)

Із формули (8.32) знаходимо υ₁ – першу космічну швидкість:

υ1 =

(8.33)

Як видно із формули (8.33), перша космічна швидкість залежить від маси планети, її радіуса та висоти над її поверхнею. Зазвичай, супутники планети (зокрема Землі) літають на невеликих висотах (h<<R), тому у формулі (8.33) висотою h можна знехтувати і формулу (8.33) записати у вигляді:

υ1 =

(8.34)

Першу космічну швидкість називають коловою швидкістю. Підставивши у формулу (8.34) заміть М і R значення маси і радіуса Землі M = 5,98∙10²⁴ кг, R=6,37∙10⁶ м, G = 6,67∙10^-11 , обчислимо першу космічну швидкість біля поверхні Землі:

υ₁ = = 7913 ≈ 8 .

Якщо швидкість руху тіла буде більшою за колову, але меншою, ніж деяка швидкість υ₂, то тіло рухатиметься по еліптичній орбіті (крива 2 на Рис.8.7). Якщо швидкість тіла дорівнюватиме швидкості υ₂, то тіло почне рухатись по параболічній орбіті (крива 3 на Рис.8.7) і покине сферу дії сил Земного тяжіння. Швидкість υ_2, за якої тіло починає рухатись по параболічній орбіті, називають параболічною швидкістю, або другою космічною швидкістю. Обчислимо значення другої космічної швидкості для планети Земля.

Для того, щоб тіло покинуло сферу сил земного тяжіння, йому необхідно надати кінетичну енергію, що дорівнює роботі сил тяжіння, виконаній під час переміщення тіла із поверхні Землі у нескінченність:

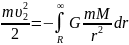
(8.35)

Інтегруючи праву частину рівняння (8.8), отримаємо:

(8.36)

Із рівняння (8.9) визначаємо другу космічну швидкість υ₂:

υ2 = , або υ2 =

(8.37)

Підставивши у формулу (8.37) замість кореня квадратного його значення із формули (8.34), отримаємо:

υ2 = υ1

(8.38)

Як видно із формули (8.38), друга космічна швидкість у разів більша, ніж перша. Друга космічна швидкість υ₂ планети Земля становить υ₂= ∙8 11 .

Третьою космічною швидкістю називають швидкість, яку потрібно надати тілу, щоб воно покинуло сферу дії сил притягання Сонця і віддалилось у Галактику.

Для того щоб тіло покинуло сферу дії сил Сонця і полетіло в Галактику, йому необхідно надати кінетичну енергію, якої буде достатньо для виконання роботи, що виконується силами притягання Сонця під час переміщення тіла із будь-якої точки орбіти Землі в нескінченність:

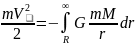
(8.39)

де M – маса Сонця, m – маса тіла, R – радіус орбіти Землі, V – третя космічна швидкість. Проінтегрувавши праву частину рівняння (8.39), визначають швидкість V

V=

(8.40)

Підставивши у (8.40) числові значення маси Сонця M=1,99∙10³⁰ кг, радіуса орбіти Землі R= 1,5∙10¹¹м, і гравітаційної сталої G, отримаємо:

V=

Зауважимо, що знайдена швидкість V – це швидкість тіла, визначена відносно Сонця. Вона може бути напрямлена у будь-якому напрямі.

Усі супутники запускають із поверхні Землі, яка рухається навколо Сонця із швидкістю, близькою до 30 . Для зменшення витрат енергії під час запуску супутників доцільно їх швидкість направляти у напрямі дотичної до орбіти Землі), бо в цьому напрямі тіло вже рухається відносно Сонця з швидкістю U = 30 . У цьому випадку відносно Землі тілу необхідно надати швидкість, що дорівнює різниці швидкостей U і V: =U- V=42-30=12 .

Зауважимо, що для того, щоб тіло покинуло Сонячну систему, воно повинно мати швидкість за межами дії сил земного тяжіння, тому початкова швидкість руху тіла повинна бути трохи більшою, ніж отримане значення швидкості .

Швидкість V_з, яку необхідно надати тілу відносно Землі для того, щоб воно покинуло Сонячну систему і полетіло в Галактику (третю космічну швидкість), знайдемо, виходячи із таких міркувань. Для того, щоб тіло покинуло сферу дії сил земного тяжіння і зберегло після цього швидкість U, його кінетична енергія в момент старту повинна дорівнювати сумі потенціальної енергії тіла на поверхні Землі і кінетичній енергії тіла, що рухається з швидкістю U:

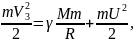
(8.41)

але

(8.42)

Підставивши замість його значення із (8.42) у формулу (8.41) і скоротивши на 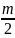, отримаємо:

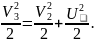
(8.43)

Із (8.43) знаходимо значення третьої космічної швидкості V₃:

V3=

(7.44)

V₃=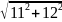 =16

Як бачимо, з урахуванням руху Землі навколо Сонця, третя космічна швидкість становить 16 кілометрів за секунду.