Частина 1. Основи механіки, молекулярної фізики і термодинаміки.

Розділ I

Фізичні основи кінематики

§1. Основні поняття кінематики поступального руху. Способи задання руху. Швидкість та прискорення.

1. Як визначити, чи рухається тіло, чи перебуває в стані спокою? Для цього вибираємо інше тіло, яке вважаємо нерухомим, і дивимось, чи змінюється положення даного тіла відносно цього “нерухомого” тіла протягом певного проміжку часу.

Тіло, прийняте за нерухоме, називають тілом відліку, пов’язану з ним систему координат та вказаний спосіб вимірювання часу називають системою відліку.

Під час вивчення руху тіл часто буває доцільно не враховувати розміри тіла. В таких випадках говорять про рух матеріальної точки. Матеріальною точкою називають тіло, розмірами якого за даних умов можна знехтувати. Наприклад, Землю можна вважати матеріальною точкою під час вивчення її руху навколо Сонця, але не можна вважати матеріальною точкою гімнаста, який виконує вправи на гімнастичних снарядах.

Кожне тіло можна уявно розділити на дрібні частини і кожну частину вважати матеріальною точкою. Тому будь-яке тіло можна вважати сукупністю матеріальних точок.

Тіло, в якому взаємне розташування частинок, з яких воно складається, не змінюється з часом, називається абсолютно твердим.

У твердому тілі будь-яка пряма, жорстко пов’язана з його частинами, завжди залишається прямою.

Рух тіла називається поступальним, якщо будь-яка пряма, жорстко пов’язана з тілом, залишаються паралельною сама собі під час руху тіла.

Під час поступального руху тіла усі його точки рухаються однаково, тому для вивчення такого руху досить вивчити рух однієї точки, що належить даному тілу.

Траєкторією руху називають лінію, вздовж якої рухається тіло (матеріальна точка).

Переміщенням матеріальної точки називають вектор, який сполучає початкове і кінцеве її положення тіла. (Рис. ).Error: Reference source not found

Пройденим шляхом називають довжину траєкторії.

Рух матеріальної точки можна задати трьома способами: векторним, координатним і

параметричним.

Рис. 1.1

1. Векторний спосіб задання руху.

Нехай матеріальна точка рухається по криволінійній траєкторії. Виберемо довільну точку О і назвемо її полюсом. Будемо проводити радіус-вектор із полюса в точку, де знаходиться тіло. Тоді кінець радіус-векто опише траєкторію, по якій рухається матеріальна точка ( 2). У цьому випадку радіус-вектор залежить від часу t і є функцією часу:

(1.1)

Якщо в момент часу тіло займало на траєкторії положення A, яке визначається радіус-вектором r_1, а в момент часу – знаходилась В ( положення тіла на траєкторії визначається радіус-вектором r₂) ( Рис.1.3), то його переміщення за проміжок часу визначиться співвідношенням:

. = = - ( 1.2)

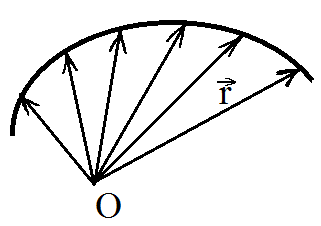
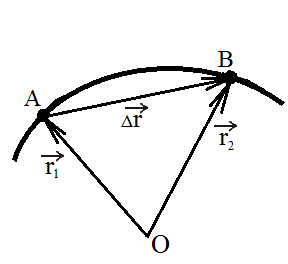
Рис. 1.2 Рис. 1.3

Середньою швидкістю матеріальної точки на ділянці траєкторії АВ називають величину, яка чисельно дорівнює відношенню довжини траєкторії АВ до часу, за який ця довжина пройдена:

,

(1.23)

де – довжина траєкторії.

Середня швидкість – це векторна величина. Вектор середньої швидкості збігається з напрямком вектора , який з’єднує початкове і кінцеве положення точки.

3

Миттєвою швидкістю називають швидкість, з якою рухається тіло рухається в даний момент часу.

Для визначення миттєвої швидкості будемо зменшувати проміжок часу . Внаслідок цього буде зменшуватися довжина пройденого шляху АВ і змінюватиметься відношення , але коли проміжок часу стане дуже малим, то швидкість V за такий малий проміжок часу не встигатиме помітно змінюватись, тому відношення буде змінюватися мало і наближатиметься до якогось цілком певного значення, яке дорівнює миттєвій швидкості. Таким чином, миттєву швидкість визначають як границю, до якої прямує відношення ,якщо прямує до нуля:

=

(1.4)

Із курсу математики відомо, що така границя дорівнює першій похідні за часом від пройденого шляху. Отже, вектор миттєвої швидкості визначають як першу похідну від вектора переміщення за часом:

= = .

(1.5)

Модуль вектора швидкості дорівнює першій похідній від пройденого шляху за часом:

V =

де S = S(t) – функція, яка визначає залежність пройденого шляху від часу.

Вектор миттєвої швидкості напрямлений вздовж дотичної до траєкторії.