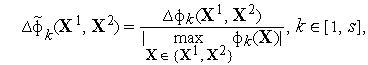1.3 Метод эпсилон-ограничений.

Рассмотрим задачу многокритериальной оптимизации

(1)

где — векторный критерий оптимальности, — частные критерии оптимальности (скалярные), — множество допустимых значений вектора варьируемых параметров.

Метод ε-ограничений относится к группе методов, основанных на сведении задачи многокритериальной оптимизации к однокритериальной многомерной задаче условной оптимизации. В методе ε-ограничений в качестве скалярного критерия оптимальности используется самый важный из частных критериев оптимальности , а остальные частные критерии учитываются с помощью ограничений типа неравенств вида .

Дополнительной информацией в методе ε-ограничений является информация о номере самого важного из частных критериев , а также информация о максимально допустимых значения частных критериев .

Таким образом, в методе -ограничений вместо задачи (1) решается задача условной оптимизации со скалярным критерием оптимальности :

(2)

где

(3)

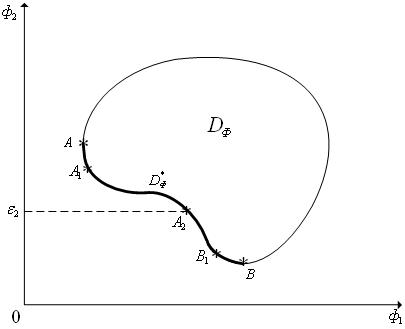
Метод ε-ограничений в значительной мере свободен от указанного выше недостатка метода весовых множителей в случае, когда множество не выпукло (см. рис. 1). На рис. 1 точка A₂ в данном методе является доступной.

Рис. 1.  Геометрическая интерпретация метода ε-ограничений: случай двух критериев; множество D_Ф не выпукло; самым важным является критерий ф₁(X); на критерий ф₂(X) наложено ограничение ф₂(X) ≤ ε₂.

Недостатком метода ε-ограничений является трудность выбора максимально допустимых значений частных критериев , которые гарантировали бы достижимость некоторого решения. Кроме того, жесткость ограничений далеко не всегда адекватна представлениям ЛПР (лица, принимающего решения) о наилучшем решении. Отметим также трудность построения в явном или неявном виде множества .

1.4 Метод справедливого компромисса.

Рассмотрим задачу многокритериальной оптимизации

(1)

где — векторный критерий оптимальности, — частные критерии оптимальности (скалярные), — множество допустимых значений вектора варьируемых параметров.

Положим, что все частные критерии имеют одинаковую важность!

Справедливым компромиссом будем называть такой компромисс, при котором относительный уровень снижения качества по одному или нескольким частным критериям не превосходит относительного уровня повышения качества по остальным частным критериям (меньше или равен). Для формализации понятия справедливого компромисса нам понадобится ввести отношение превосходства на множестве Парето.

Пусть во множестве Парето задачи (1) даны две точки , и значения всех частных критериев оптимальности в них . Введем меру относительного изменения (снижения – знак "минус" или повышения – знак "плюс") качества решения по каждому из этих критериев

(2)

где — абсолютные изменения значений частных критериев оптимальности при переходе от решения к решению . Вычислим максимальное снижение качества решения при переходе от решения к решению

(3)

Аналогично вычислим максимальное повышение качества решения при переходе от решения к решению

(4)

Будем говорить, что решение превосходит решение , и писать

(5)

С другой стороны, будем говорить, что решение превосходит решение , и писать

(6)

Упрощенная схема метода справедливого компромисса.

Рассмотрим основные этапы метода справедливого компромисса.

1. Полагаем счетчик числа итераций .

2. Тем или иным способом выбираем из множества Парето задачи 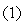решение .

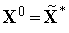3. Вычисляем значения всех частных критериев оптимальности в точке .

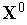4. Тем или иным способом выбираем из множества Парето задачи (1) решение .

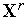5. Вычисляем значения всех частных критериев оптимальности в точке .

6. По формулам (2), (3), (4), (5), (6) из числа решений 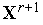, находим превосходящее решение. Обозначим его .

7. Если условие окончания итераций выполнено (см. ниже), то принимаем точку в качестве приближенного решения задачи (1) и заканчиваем вычисления. Иначе полагаем 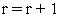и переходим к п.3

В простейшем случае выбор решений может быть произведен случайным образом. В качестве условия окончания итераций в этом случае может быть использовано достижение заданного количества итераций. Выбор решений может быть произведен также с помощью полного перебора узлов какой-либо сетки, покрывающей множество .

Поскольку метод справедливого компромисса использует относительные изменения частных критериев оптимальности, этот метод инвариантен к масштабу измерения частных критериев, т.е. не требуется их нормализация.