ТС и СА

Тема: Методы многокритериальной оптимизации

Содержание

Введение

1. Методы многокритериальной оптимизации

1.1 Множество Парето

1.2 Метод весовых множителей

1.3 Метод эпсилон-ограничений

1.4 Метод справедливого компромисса

1.5 Метод приближения к идеальному решению

1.6 Метод последовательных уступок

2. Пример решения задачи многокритериальной оптимизации

Введение.

В практике человеческой деятельности, будь то профессиональная сфера или повседневная жизнь, постоянно возникают задачи выбора, предполагающие в результате принятие решения. Только в ряде случаев человек – лицо, принимающее решение (ЛПР) – осуществляет выбор (принимает решение) интуитивно, опираясь на собственный опыт и здравый смысл, а решение более сложных задач требует особого подхода, так как в данном случае задача принятия решения представляет собой, по сути, уже оптимизационную задачу. Таким образом, выбор решения в сложных ситуациях требует научной поддержки.

Для того чтобы осуществить «хороший» выбор, т.е. выбрать наилучшее решение, наиболее точно соответствующее достижению цели ЛПР, необходимо располагать предварительным множеством альтернатив-решений, из которых и предстоит сделать окончательный выбор. Множество альтернатив должно быть по возможности наиболее полным и представительным, учитывающим все возможные варианты решения. Второй неотъемлемой составляющей является способ сравнения альтернатив между собой – критерий оценки их качества, позволяющий осуществлять непосредственный отбор наиболее предпочтительных альтернатив из первоначального множества. В этом и заключается суть многокритериальной оптимизации.

МНОГОКРИТЕРИАЛЬНАЯ ОПТИМИЗАЦИЯ – Методы решения задач, которые состоят в поиске лучшего (оптимального) решения, удовлетворяющего нескольким несводимым друг к другу критериям.

1. Методы многокритериальной оптимизации.

Многокритериальная оптимизация подразделяется на нескольких методов, рассмотрим некоторые из них.

1.1 Множество Парето.

Введем понятие пространства критериев . Пространство критериев имеет размерность (по числу частных критериев) и образуется ортогональными осями координат, вдоль которых откладываются значения частных критериев оптимальности .

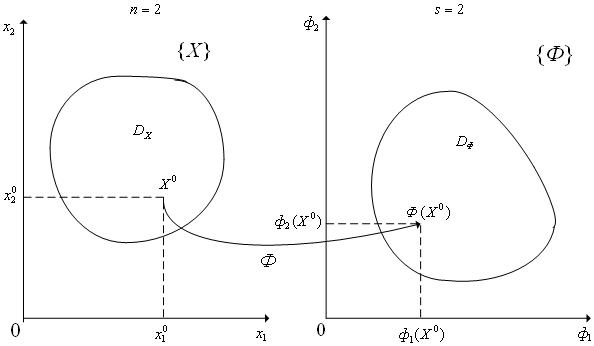
Векторный критерий оптимальности выполняет отображение множества допустимых значений в некоторую область , где — пространство варьируемых параметров (см. рис. 1).

Рис. 1.  К отображению векторным критерием оптимальности Φ(X) множества допустимых значений D_X пространства варьируемых параметров {X} в область D_Φ пространства критериев {Φ}. Случай n=2, s=2.

Введем на множестве отношение предпочтения.

Отношение предпочтения . Будем говорить, что вектор предпочтительнее вектора , и писать , если среди равенств и неравенств

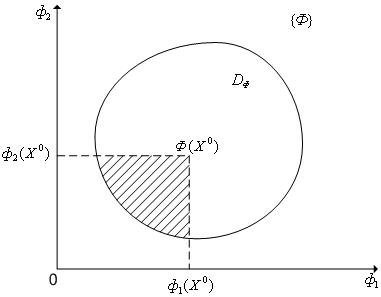
имеется хотя бы одно строгое неравенство (см. рис. 2).

Аналогично на множестве введем отношение доминирования: будем говорить, что векторный критерий оптимальности доминирует векторный критерий оптимальности , и писать , если (см. рис. 2).

Примечание 1

Введенные отношение предпочтения и отношение доминирования являются транзитивными, т.е.

если и , то ;

если ) и ( , то ( .

Рис. 2.  К понятию отношения предпочтения и отношения доминирования (s = 2). Для всех точек заштрихованной области Ф(X¹) ⊳ Ф(X²), т.е. заштрихованной области пространства критериев соответствуют векторы варьируемых параметров X ∈ D_Ф, для которых X¹ ⊱ X².

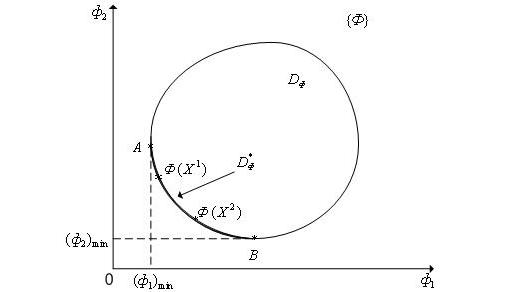
Выделим из множества подмножество точек, для которых нет точек, их доминирующих. Множество , соответствующее , называется множеством Парето (переговорным множеством, областью компромисса) — см. рис. 3. Поскольку множество D_Ф на рисунке является выпуклым, то множество D - есть часть границы множества D_Ф — дуга AB, в которой точка A соответствует (ф₂)_min, а точка B — (ф₁)_min. Среди точек (X¹) D^*_Ф, (X²) D^*_Ф нет более предпочтительных, поскольку ф₁(X¹) > ф₁(X²), но ф₂(X¹) > ф₂(X²).

Таким образом, если , то

Другими словами множество Парето можно определить как множество, в котором значение любого из частных критериев оптимальности можно улучшить только за счет ухудшения других частных критериев – любое из решений, принадлежащее множеству Парето, не может быть улучшено одновременно по всем частным критериям.

Рис. 3.  К определению множества Парето (s = 2).