Одновыборочный t-критерий

Применяется для проверки нулевой гипотезы   о равенстве математического ожидания   некоторому известному значению  .

Очевидно, при выполнении нулевой гипотезы  . С учётом предполагаемой независимости наблюдений  . Используя несмещенную оценку дисперсии   получаем следующую t-статистику:

При нулевой гипотезе распределение этой статистики  . Следовательно, при превышении критического значения нулевая гипотеза отвергается.

Двухвыборочный t-критерий для независимых выборок]

Пусть имеются две независимые выборки объемами   нормально распределенных случайных величин  . Необходимо проверить по выборочным данным нулевую гипотезу равенстве математических ожиданий этих случайных величин  .

Рассмотрим разность выборочных средних  . Очевидно, если нулевая гипотеза выполнена  . Дисперсия этой разности равна исходя из независимости выборок:  . Тогда используя несмещенную оценку дисперсии   получаем несмещенную оценку дисперсии разности выборочных средних:  . Следовательно, t-статистика для проверки нулевой гипотезы равна

Эта статистика при справедливости нулевой гипотезы имеет распределение  , где 

Случай одинаковой дисперсии

В случае, если дисперсии выборок предполагаются одинаковыми, то

Тогда t-статистика равна:

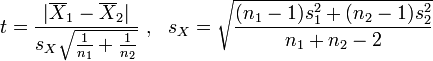
Эта статистика имеет распределение 

Двухвыборочный t-критерий для зависимых выборок[править

Для вычисления эмпирического значения t-критерия в ситуации проверки гипотезы о различиях между двумя зависимыми выборками (например, двумя пробами одного и того же теста с временным интервалом) применяется следующая формула:

где   — средняя разность значений,   — стандартное отклонение разностей, а n — количество наблюдений

Эта статистика имеет распределение  .

Проверка линейного ограничения на параметры линейной регрессии[править]

С помощью t-теста можно также проверить произвольное (одно) линейное ограничение на параметры линейной регрессии, оцененной обычным методом наименьших квадратов. Пусть необходимо проверить гипотезу  . Очевидно, при выполнении нулевой гипотезы  . Здесь использовано свойство несмещенности МНК-оценок параметров модели  . Кроме того,  . Используя вместо неизвестной дисперсии ее несмещенную оценку   получаем следующую t-статистику:

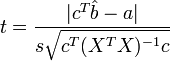
Эта статистика при выполнении нулевой гипотезы имеет распределение  , поэтому если значение статистики выше критического, то нулевая гипотеза о линейном ограничении отклоняется.

Проверка гипотез о коэффициенте линейной регрессии

Частным случаем линейного ограничения является проверка гипотезы о равенстве коэффициента   регрессии некоторому значению  . В этом случае соответстующая t-статистика равна:

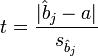
где   — стандартная ошибка оценки коэффициента — квадратный корень из соответствующего диагонального элемента ковариационной матрицы оценок коэффициентов.

При справедливости нулевой гипотезы распределение этой статистики —  . Если значение статистики выше критического значения, то отличие коэффициента от  является статистически значимым (неслучайным), в противном случае — незначимым (случайным, то есть истинный коэффициент вероятно равен или очень близок к предполагаемому значению  )

Замечание[править | править исходный текст]

Одновыборочный тест для математических ожиданий можно свести к проверке линейного ограничения на параметры линейной регрессии. В одновыборочном тесте это «регрессия» на константу. Поэтому   регрессии это и есть выборочная оценка дисперсии изучаемой случайной величины, матрица   равна  , а оценка «коэффициента» модели равна выборочному среднему. Отсюда и получаем выражение для t-статистики, приведенное выше для общего случая.

Аналогично можно показать, что двухвыборочный тест при равенстве дисперсий выборок также сводится к проверке линейных ограничений. В двухвыборочном тесте это «регрессия» на константу и фиктивную переменную, идентифицирующую подвыборку в зависимости от значения (0 или 1):  . Гипотеза о равенстве математических ожиданий выборок может быть сформулирована как гипотеза о равенстве коэффициента b этой модели нулю. Можно показать, что соответствующая t-статистика для проверки этой гипотезы равна t-статистике, приведенной для двухвыборочного теста.

Также к проверке линейного ограничения можно свести и в случае разных дисперсий. В этом случае дисперсия ошибок модели принимает два значения. Исходя из этого можно также получить t-статистику, аналогичную приведенной для двухвыборочного теста.

Случайная величина — это величина, которая принимает в результате опыта одно из множества значений, причём появление того или иного значения этой величины до её измерения нельзя точно предсказать.

Биномиа́льное распределе́ние в теории вероятностей — распределение количества «успехов» в последовательности из   независимых случайных экспериментов, таких, что вероятность «успеха» в каждом из них постоянна и равна  .

Для применения данного критерия необходимо, чтобы исходные данные имели нормальное распределение. В случае применения двухвыборочного критерия для независимых выборок также необходимо соблюдение условия равенства дисперсий. Существуют, однако, альтернативы критерию Стьюдента для ситуации с неравными дисперсиями.

Требование нормальности распределения данных является необходимым для точного  -теста. Однако, даже при других распределениях данных возможно использование  -статистики. Во многих случаях эта статистика асимптотически имеет стандартное нормальное распределение —  , поэтому можно использовать квантили этого распределения. Однако, часто даже в этом случае используют квантили не стандартного нормального распределения, а соответствующего распределения Стьюдента, как в точном  -тесте. Асимптотически они эквивалентны, однако на малых выборках доверительные интервалы распределения Стьюдента шире и надежнее.

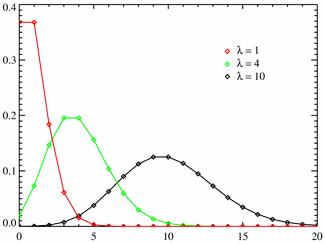
Пуассоновское распределение (дискретное)

Распределение Пуассона моделирует случайную величину, представляющую собой число событий, произошедших за фиксированное время, при условии, что данные события происходят с некоторой фиксированной средней интенсивностью и независимо друг от друга.

При условии  закон распределения Пуассона является предельным случаем биномиального закона. Так как при этом вероятность   события A в каждом испытании мала, то закон распределения Пуассона называют часто законом редких явлений.

Ряд распределения:

	0	1	…..	k	…..
			…..		…..

Вероятности вычисляются по формуле Пуассона:  .

Числовые характеристики:  ,  , 

Разные многоугольники распределения при  .