
- •По дисциплине «физика»
- •Часть 3: Колебания и волны. Оптика
- •Введение
- •Правила оформления работы
- •Варианты контрольных работ вариант 1
- •Вариант 2
- •Вариант 3
- •Вариант 4
- •Вариант 5
- •Вариант 6
- •Вариант 7
- •Вариант 8
- •Вариант 9
- •Вариант 10
- •Вариант 11
- •Вариант 12
- •Вариант 13
- •Вариант 14
- •Вариант 15
- •Вариант 16
- •Вариант 17
- •Вариант 18
- •Вариант 19
- •Вариант 20
- •Контрольная работа № 3
- •Вариант 1
- •Задача №1
- •Задача №2
- •Задача №3
- •Задача №4
- •Задача №5
- •Задача №6
- •Задача №7
- •Задача №8
- •Задача №9
- •Задача №10
- •Решение:
- •Список используемой литературы:
- •Литература Основная
- •Дополнительная
- •426003, Г. Ижевск, ул. Сивкова, 12а.
Задача №5
Условие: Свинцовый шарик ( = 11.3 г/см3) диаметром 0.5 см помещен в глицерин ( = 1.26 г/см3). Определите заряд шарика, если в однородном электростатическим поле шарик оказался взвешенным в глицерине. Электростатическое поле направлено вертикально вверх и его напряженность Е = 4 кВ/с.
Дано
|
Решение
Подставим (2) в (1):
|
||||
Ответ:
|
|||||
Задача №6
Условие: Определите плотность тока, если за 2 с через проводник сечением 1.6 мм2 прошло 21019 электронов.
Дано
|
Решение
Плотность тока:
|
||||
Ответ:
|
|||||
Задача №7
Условие: Определите минимальную скорость электрона, необходимую для ионизации атома водорода, если потенциал ионизации атома водорода Ui = 13.6 В.
Дано
|
Решение
|
||||
Ответ:
|
|||||
Задача №8
Условие: Электрон движется в однородном магнитном поле с индукцией В = 0.1 Тл по окружности. Определите угловую скорость вращения электрона.
Дано
|
Решение На электрон со стороны магнитного поля действует сила Лоренца
Благодаря которой
орбита электрона – окружность
|
||||
Ответ:
|
|||||
Задача №9
Условие: В однородное магнитное поле с индукцией В = 0.3 Тл помещена прямоугольная рамка с подвижной стороной, длина которой l = 15 см. Определите ЭДС индукции, возникающей в рамке, если ее подвижная сторона перемещается перпендикулярно линиям магнитной индукции со скоростью v = 10 м/с.
Дано
|
Решение
|
||||
Ответ:
ЭДС индукции, возникающая в рамке с
подвижной стороной равна
|
|||||
Задача №10
Условие: Докажите с помощью одного из уравнений Максвелла, что переменное во времени магнитное поле не может существовать без электрического поля.

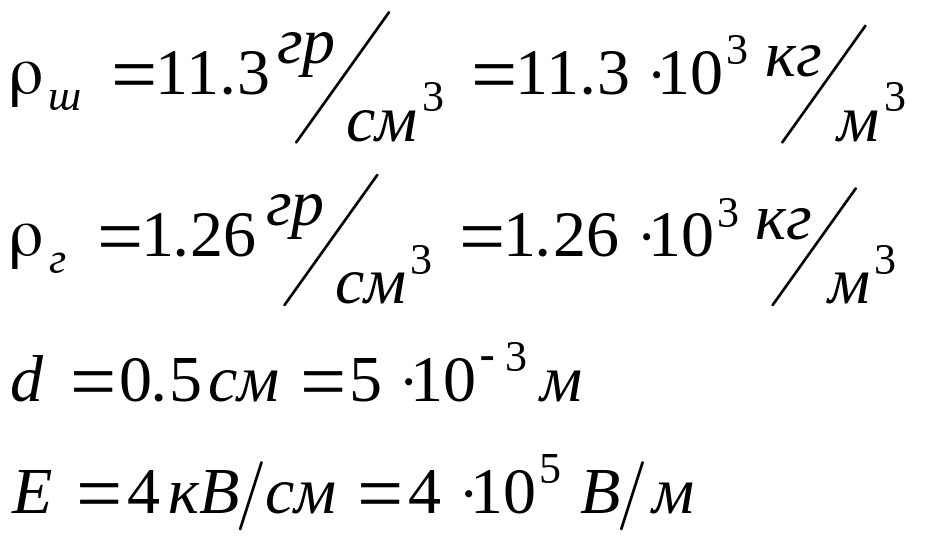
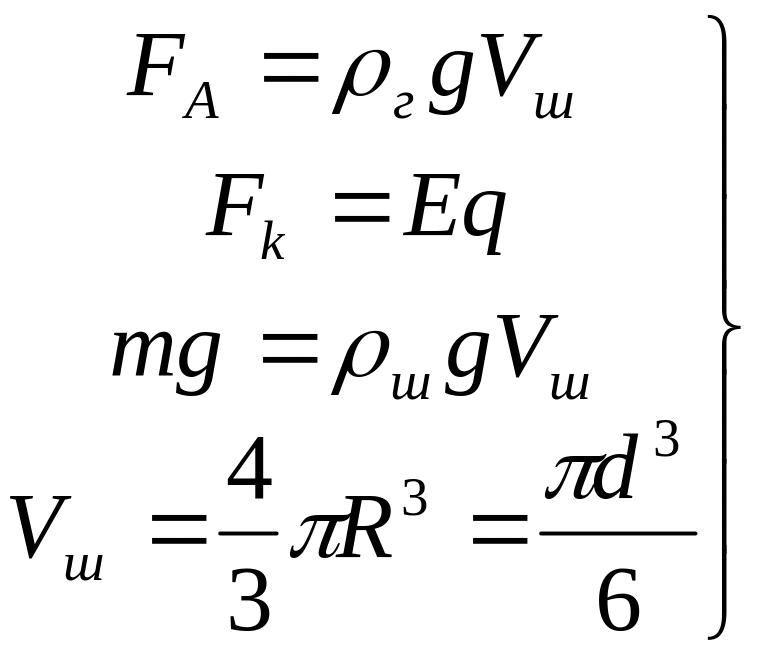 (2)
(2)


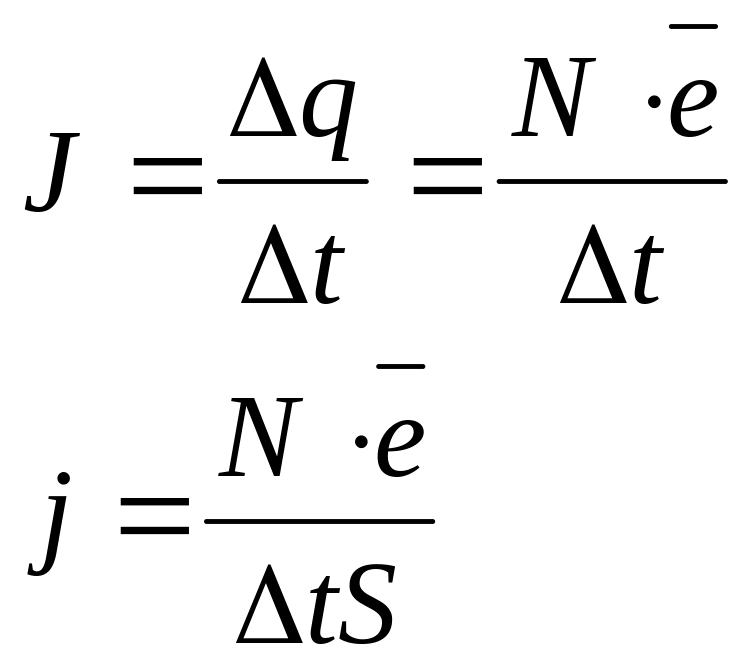

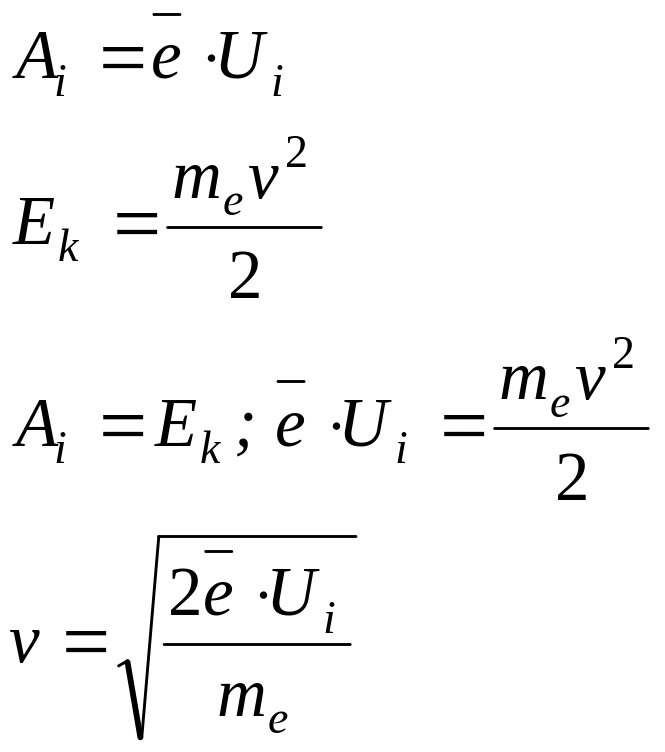
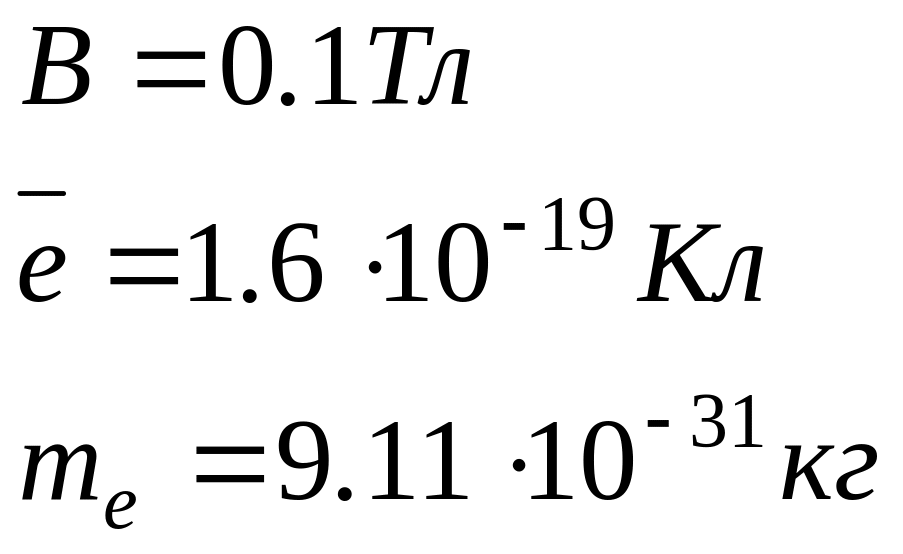
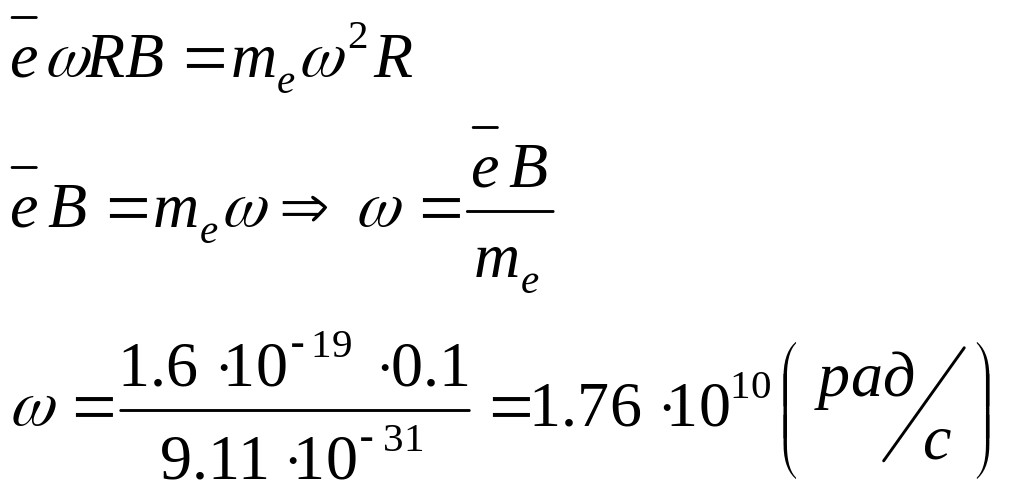
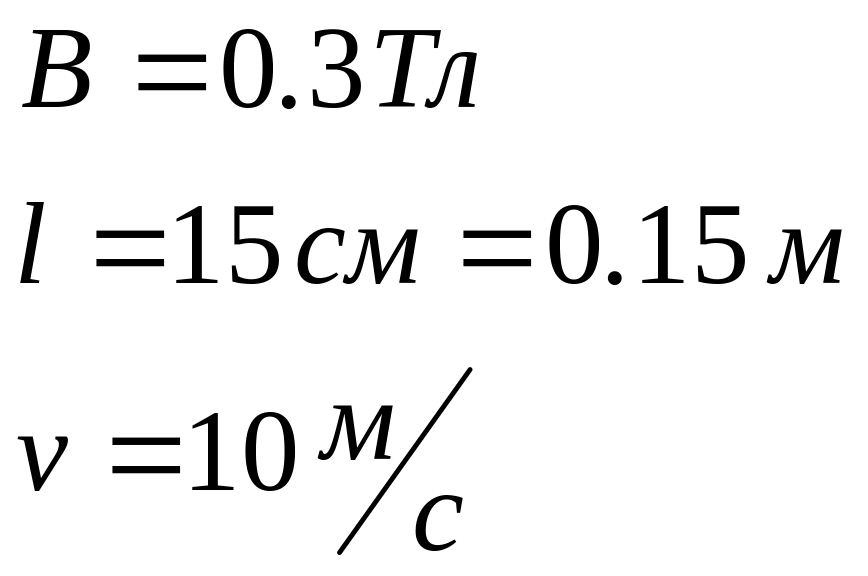
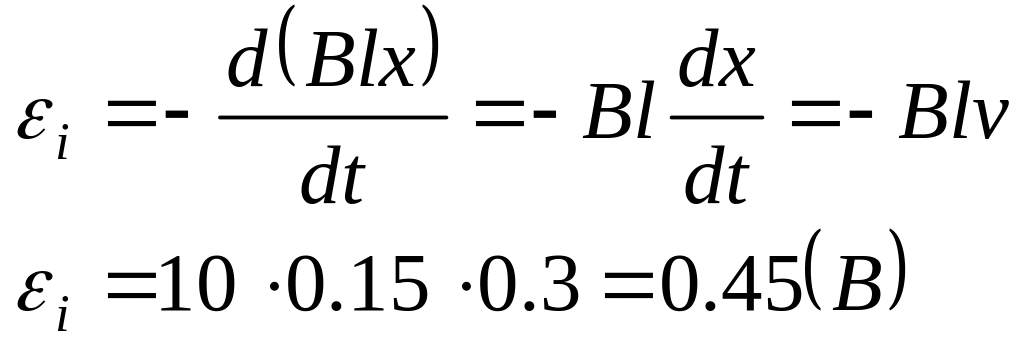 тогда по модулю
тогда по модулю