20. Понятие сочлененной системы тел.

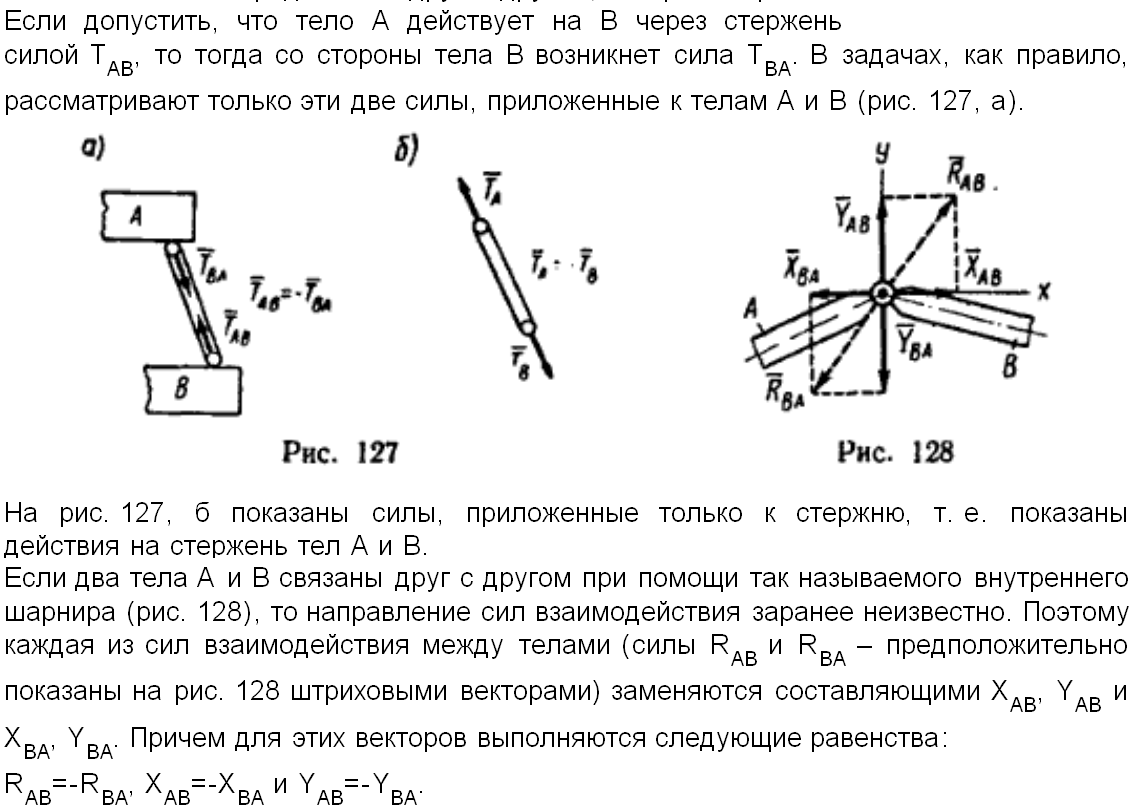
21. Статически определимые и статически неопределимые системы тел (конструкции).

Если при рассмотрении заданной системы, находящейся в равновесном состоянии от действия заданных внешних нагрузок, все реакции в связях закрепления, а также внутренние усилия в ее элементах, можно определить только по методу сечений, без использования дополнительных условий, то такая система называется статически определимой.

В реальной практике встречаются такие конструкции при расчете которых одних лишь уравнений равновесия оказывается недостаточно, в связи с чем требуется формулирование дополнительных уравнений, связанных с условиями деформирования конструкции.

Системы, в которых количество наложенных связей больше, нежели число независимых уравнений равновесия, называются статически неопределимыми.

По сравнению со статически определимыми системами, в статически неопределимых системах имеются дополнительные связи, которые называются лишними.

Термин “лишние связи” является условным. Эти связи являются лишними с точки зрения расчетных предпосылок. В действительности эти связи создают дополнительные резервы для конструкций, как в плане обеспечения её жесткости, так и прочности.

Степень статической неопределимости равна разности между числом неизвестных и числом полезных уравнений равновесия.

Для раскрытия статической неопределимости существуют разные способы:

1.Метод сил. Здесь в качестве неизвестных рассматриваются усилия - силы и моменты.

2.Метод перемещений. Неизвестными являются деформационные факторы - углы поворотов и линейные смещения.

3.Смешанный метод. Здесь часть неизвестных представляет собой усилия, а другая часть - перемещения.

4. Комбинированный метод. Используется при расчете симметричных систем на несимметричные нагрузки. Оказывается, что на симметричную составляющую заданной нагрузки систему целесообразно рассчитывать методом перемещений, а на обратносимметричную составляющую - методом сил.

Заметим лишь, что всякая реакция возникает в местах наложения внешних связей (ограничений движения системы). Нет ограничения — нет реакции. Есть ограничение — есть реакция. В то же время любая наложенная связь (любое ограничение движения) позволяет составить дополнительное уравнение, называемое уравнением совместности перемещений. В результате появляется возможность сделать число уравнений равным числу неизвестных и решить систему уравнений.

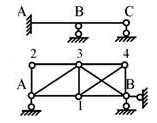
Пример статически неопределимых систем

22. Равновесие тел при наличии трения скольжения.

Е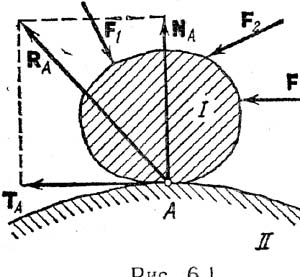 сли два тела I и II (рис. 6.1) взаимодействуют друг с другом, соприкасаясь в точке А, то всегда реакцию R_A, действующую, например, со стороны тела II и приложенную к телу I, можно разложить на две составляющие: N_A, направленную по общей нормали к поверхности соприкасающихся тел в точке А, и Т_А, лежащую в касательной плоскости.

С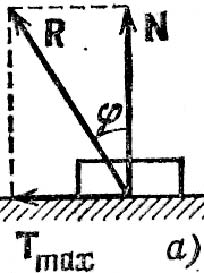 оставляющая N_A называется нормальной реакцией, сила Т_А называется силой трения скольжения — она препятствует скольжению тела I по телу II. В соответствии с аксиомой 4 (третьим законом Ньютона) на тело II со стороны тела I дей­ствует равная по модулю и противоположно направленная сила реакции. Ее составляющая, перпендикулярная касательной плоскости, называется силой нормального давления. Сила трения Т_А = 0, если соприкасающиеся поверхности идеально гладкие. В реальных условиях поверхности шероховаты и во многих случаях пренебречь силой трения нельзя. Максимальная сила трения приближенно пропорциональна нормальному давлению, т. е. Tmax=fN– закон Амонтона—Кулона. Коэффициент f называется коэффициентом трения скольжения. Его значение не зависит от площади соприкасающихся поверхностей, но зависит от материала и степени шероховатости соприкасающихся поверхностей.

Силу трения можно вычислить по ф-ле T=fN только если имеет место критический случай. В других случаях силу трения следует определять из уравнений равновесия. На рисунке показана реакция R (здесь активные силы стремятся сдвинуть тело вправо). Угол j между предельной реакцией R и нормалью к поверхности называется углом трения. tgφ=T_max/N=f.

Геометрическое место всех возможных направлений предельной реакции R образует коническую поверхность — конус трения. Если коэффициент трения f во всех направлениях одинаков, то конус трения будет круговым. В тех случаях, когда коэффициент трения f зависит от направления возможного движения тела, конус трения не будет круговым. Если равнодействующая активных сил находится внутри конуса трения, то увеличением ее модуля нельзя нарушить равновесие тела; для того чтобы тело начало движение, необходимо (и достаточно), чтобы равнодействующая активных сил F находилась вне конуса трения.

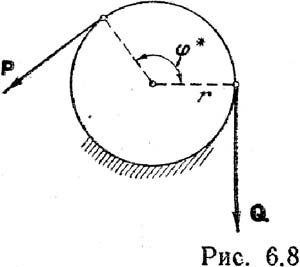
Рассмотрим трение гибких тел. Формула Эйлера помогает найти наименьшую силу P, способную уравновесить силу Q. P=Qe^-fj*. Можно так же найти такую силу P, способную преодолеть сопротивление трения вместе с силой Q. В этом случае в формуле Эйлера поменяется только знак f: P=Qe^fj*.