14.Теорема о моменте равнодействующей (теорема Вариньона).
15. Частные случаи приведения плоской системы сил.
16. Сосредоточенные и распределенные силы.
На рисунке 1, а приведена равномерно распределенная по длине AB нагрузка интенсивностью q , измеряемая в Н/м. Эта нагрузка может быть заменена сосредоточенной силой
Q = q⋅ AB [Н],
приложенной в середине отрезка AB . На рисунке 1, б показана равномерно убывающая (возрастающая) нагрузка, которая может быть заменена равнодействующей силой
Q = 1/2 qmax⋅ AB,
приложенной в точке C , причем AC = 2/3 AB .
В произвольном случае, зная функцию q(x) (рисунок 1., в), рассчитываем эквивалентную силу
Эта сила приложена в центре тяжести площади, ограниченной сверху от балки AB линией q(x).
17. Пространственная система сил. Понятие динамического винта.
Система сил, действующих на абсолютно твердое тело, линии действия которых направлены в пространстве произвольно, называется произвольной пространственной системой сил.
Существует два способа задания такой системы сил: 1 - графический; 2 - аналитический. При графическом способе задаётся модуль вектора силы и углы, определяющие направление этого вектора в трехмерной декартовой системе координат. Рассмотрим это на примере одной силы. рис. 1.51.
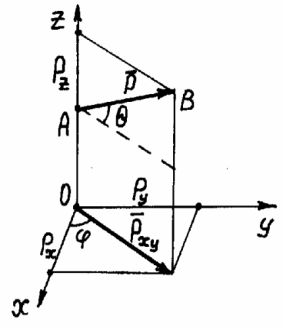
Рис. 1.51. Схема графического задания Рис. 1.52. Схема к аналитическому заданию
положения силы
в пространстве пространственной
силы
При аналитическом
способе задания пространственной
системы сил (рис. 1.52) каждая сила задается
в виде векторного уравнения 
.
Здесь 
-
единичные векторы осей (орты); 
,
,
.
Вариант приведения произвольной пространственной системы сил к единому центру
если 
и 
,
и вектор 
параллелен вектору 
,
система приводится к силе
и
паре с моментом
,
векторы которых приложены в одной точке
и направлены вдоль одной линии. Такая
совокупность называется динамическим
винтом, или «динамой» (рис. 1.60).
Схема динамического винта
|
|
18. Частные случаи приведения пространственной системы сил к простейшему виду.
19. Равновесие произвольной пространственной системы сил, случай параллельных сил.
Для равновесия
произвольной пространственной системы
сил необходимо и достаточно, чтобы: 
и 
.
Эти условия выполняются только тогда,
когда:
.
(1.43)
(1.44)
Из этого следует:
;
;
,
Равенство нулю проекций сил на оси координат отражает отсутствие перемещения тела вдоль координатных осей. Равенства нулю моментов сил относительно осей координат означает отсутствие вращений тела относительно этих осей.
Если все силы
параллельны, например, оси 
,
то условие равновесия запишется так:
(1.45)
Для равновесия пространственной системы параллельных сил необходимо и достаточно, чтобы сумма проекций этих сил на ось, параллельную силам, и суммы их моментов относительно двух других координатных осей были равны нулю.