4. Аксиомы статики.

Все теоремы и уравнения статики выводятся из нескольких исходных положений, принимаемых без математических доказательств и называемых аксиомами или принципами статики. Аксиомы статики представляют собой результат обобщений многочисленных опытов и наблюдений над равновесием и движением тел, неоднократно подтвержденных практикой.

А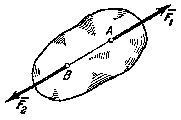 ксиома 1. Если на свободное абсолютно твердое тело действуют две силы, то тело может находиться в равновесии тогда и только тогда, когда эти силы равны по модулю (F₁ = F₂) и направлены вдоль одной прямой в противоположные стороны. Аксиома 1 определяет простейшую уравновешенную систему сил, так как опыт показывает, что свободное тело, на которое действует только одна сила, находиться в равновесии не может.

А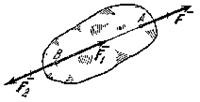 ксиома 2. Действие данной системы, сил на абсолютно твердое тело не изменится, если к ней прибавить или от нее отнять уравновешенную систему сил. Эта аксиома устанавливает, что две системы сил, отличающиеся на уравновешенную систему, эквивалентны друг другу.

Следствие из 1-й и 2-й аксиом. Действие силы на абсолютно твердое тело не изменится, если перенести точку приложения силы вдоль ее линии действия в любую другую точку тела.

А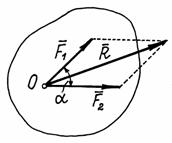 ксиома 3 (аксиома параллелограмма сил). Две силы, приложенные к телу в одной точке, имеют равнодействующую, приложенную в той же точке и изображаемую диагональю параллелограмма, построенного на этих силах, как на сторонах.

Вектор , равный диагонали параллелограмма, построенного на векторах и , называется геометрической суммой векторов и : = + . Конечно, + . Такое равенство будет соблюдаться только при условии, что эти силы направлены по одной пря­мой в одну сторону. Если же векторы сил окажутся перпендикулярными, то , если нет то равнодействующая . Аксиому 3 можно еще формулировать так: две силы, приложенные к телу в одной точке, имеют равнодействующую, равную геометрической (векторной) сумме этих сил и приложенную в той же точке.

А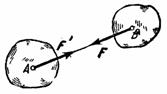 ксиома 4. При всяком действии одного материального тела на другое имеет место такое же по величине, но противоположное по направлению противодействие. Закон о равенстве действия и противодействия является одним из основных законов механики. Из него следует, что если тело А действует на тело В с силой , то одновременно тело В действует на тело А с такой же по модулю и направленной вдоль той же прямой, но противоположную сторону силой =- . Однако силы и не образуют уравновешенной системы сил, так как они приложены к разным телам.

Аксиома 5 (принцип отвердевания). Равновесие изменяемого (деформируемого) тела, находящегося под действием данной системы сил, не нарушится, если тело считать отвердевшим (абсолютно твердым).

Высказанное в этой аксиоме утверждение очевидно. Например, ясно, что равновесие цепи не нарушится, если ее звенья считать сваренными друг с другом и т. д.

5. Связи и их реакции. Принцип освобождаемости от связей.

Тело, которое может совершать из данного положения любые перемещения в пространстве, называется свободным. Тело, перемещениям которого препятствуют какие-нибудь другие, скрепленные или соприкасающиеся с ним тела, называется несвободным. Все то, что ограничивает перемещение данного тела, называют связью.

Сила, с которой данная связь действует на тело, препятствующая тем или иным его перемещениям, называется реакцией связи. Реакция связи направлена в сторону противоположную той, куда связь не дает перемещаться телу.

Принцип освобождаемости от связей: несвободное твердое тело можно рассматривать как свободное, если его мысленно освободить от связей, заменив их действие реакциями. В статике этот принцип позволяет рассматривать равновесие несвободного твердого тела как свободного под действием активных (заданных) сил и реакций связей. Рассмотрим наиболее часто встречающиеся типы связей на плоскости и направления их реакций.

1. Гладкая плоскость (поверхность) или опора

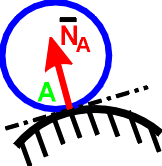Реакция N гладкой плоскости (поверхности) или опоры направлена по общей нормали к поверхностям соприкасающихся тел в точке их касания и приложена к этой точке.

2. Гибкая нить (провода, канаты, цепи, ремни)

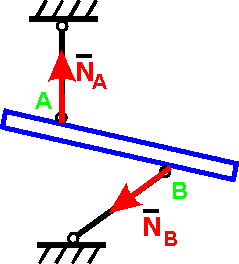Реакция Т направлена вдоль нити к точке подвеса.

3. Невесомый стержень с шарнирами

Реакция N невесомого стержня направлена вдоль стержня. Обычно реакция N изображается от тела по стержню, в предположении, что в равновесии стержень растянут.

4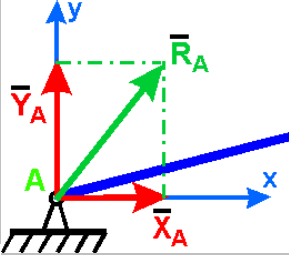 . Неподвижный цилиндрический шарнир или подшипник

Реакция RA цилиндрического шарнира может иметь любое направление в плоскости, перпендикулярной оси вращения, т. е. в плоскости А_ХУ. Обычно ее раскладывают на две составляющие Х_А и Y_A по двум взаимноперпендикулярным направлениям.

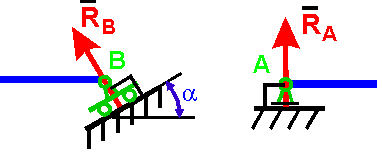
5. Шарнирно-подвижная опора (опора на катках)

Реакция R проходит через ось шарнира и направлена перпендикулярно к опорной плоскости.

6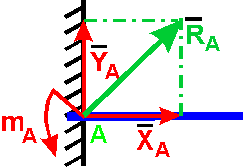 . Жесткая заделка

Нахождение реакции жесткой заделки сводится к определению составляющих Х_А и Y_A препятствующих линейному перемещению балки в плоскости действия сил, и алгебраической величине момента m_A, препятствующего вращению балки под действием приложенных к ней сил.

6. Понятие о главном векторе. Основные способы его вычисления.

Системой сходящихся сил называется система сил, линии действия которых пересекаются в одной точке. Две силы, сходящиеся в одной точке, согласно третьей аксиоме статики можно заменить одной силой – равнодействующей.

Решение многих задач статики связано с операцией сложения векторов, в частности, сил.

Главный вектор системы сил – величина, равная геометрической сумме сил системы. Главный вектор системы сил не следует путать с равнодействующей. Равнодействующая – всегда главный вектор, а главный вектор равен равнодействующей, если система сил является сходящейся.

Равнодействующую плоской системы сходящихся сил можно определить графически и графоаналитически.

Сложение двух сил. При графическом определении равнодействующей на чертеже и выбранном масштабе изображаются силы, затем они складываются по правилу параллелограмма. По длине диагонали параллелограмма, учитывая выбранный масштаб, определяется равнодействующая, равная сумме слагаемых сил. Точность определения равнодействующей зависит в этом случае от точности построения силового треугольника.

Г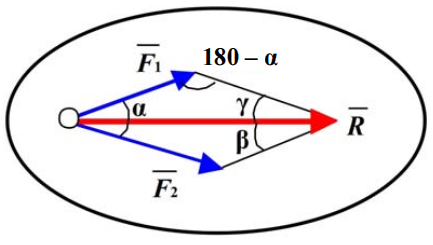 рафоаналитический способ сложения сил позволяет более точно определить равнодействующую, используя тригонометрические зависимости:

- теорему косинусов:

или

- теорему синусов:

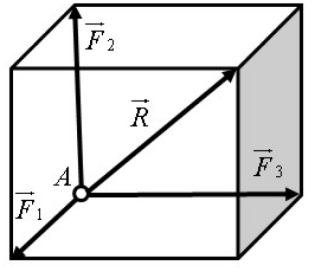
Сложение трех сил, не лежащих в одной плоскости: геометрическую сумму трех сил не лежащих в одной плоскости, изображают диагональю параллелепипеда, построенного на этих силах (правило параллелепипеда).

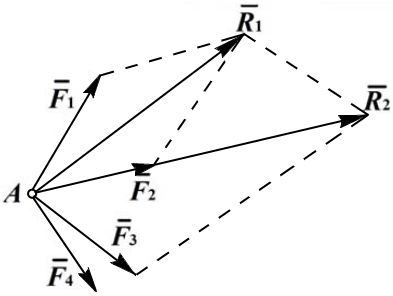
Сложение системы сил. Сложение плоской системы сходящихся сил осуществляется либо путём последовательного сложения сил с построением промежуточной равнодействующей (1), либо путём построения силового многоугольника (2).

1 2