Коррекция частотной характеристики.
Вследствие наличия паразитных емкостей и многокаскадной структуры ОУ по своим частотным свойствам аналогичен фильтру нижних частот высокого порядка. Системы такого рода, имеющие большой коэффициент усиления, при наличии обратной связи склонны к самовозбуждению (потере устойчивости). Это проявляется в том, что даже при отсутствии сигнала на входе системы на ее выходе могут возникать стационарные или прерывистые колебания относительно большой амплитуды, вплоть до полного размаха выходного напряжения. В результате схема, спроектированная, казалось бы, по всем правилам радиотехники, оказывается неработоспособной. Вопрос этот чрезвычайно важен, поэтому остановимся на нем подробнее.
Поведение ОУ в переходных процессах при малых изменениях сигналов можно математически описать линейным дифференциальным уравнением. Преобразование этого уравнения по Лапласу дает возможность представить отношение переменных величин на входе и выходе усилителя в удобной алгебраической форме
причем на практике в данном случае всегда п > т. Нули полинома в числителе называются нулями передаточной функции, а нули полинома в знаменателе — ее полюсами. Из теории систем автоматического управления известно, что устойчивость системы с обратной связью (в нашем случае усилителя) определяется расположением на комплексной плоскости корней характеристического уравнения
Если все без исключения корни уравнения располагаются в левой полуплоскости — усилитель с обратной связью устойчив. Если хотя бы один из корней этого уравнения находится в правой полуплоскости — усилитель неустойчив.
Подставив в первоначальную формулу s=j, получим частотную характеристику усилителя
Частотные характеристики оу.
Наиболее удобно исследовать устойчивость усилителей по диаграммам Боде, на которых амплитудно-частотная и фазо-частотная характеристики изображаются асимптотически в логарифмическом масштабе, и называются соответственно ЛАЧХ и ЛФЧХ. Эти характеристики легко определяются экспериментально и позволяют достаточно просто и наглядно судить об устойчивости конкретного ОУ и осуществить подбор корректирующих цепей. Типичные асимптотические ЛАЧХ и ЛФЧХ ОУ без частотной коррекции в функции циклической частоты f=/2 приведены на рисунке.
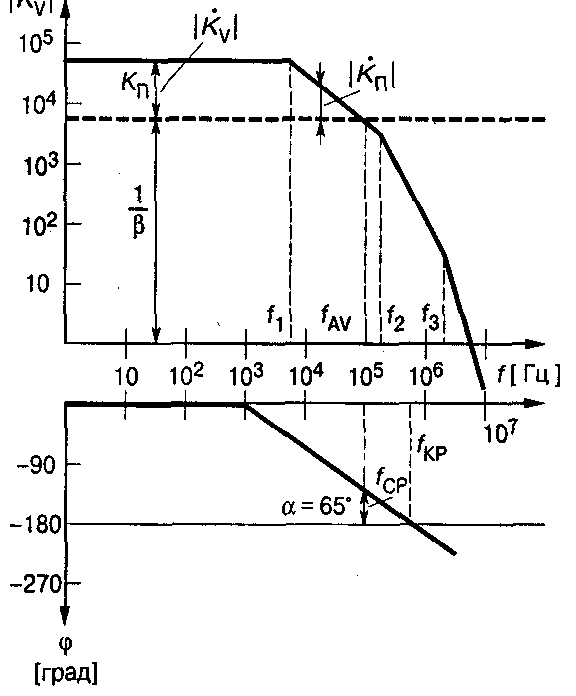
Типичные логарифмические амплитудно-частотная и
фазо-частотная характеристики некорректированного ОУ
Асимптотической называется характеристика, образованная соединенными отрезками касательных, проведенных к точной ЛАЧХ с наклоном, кратным 20 дБ/дек. Асимптотическая ЛАЧХ позволяет легко определить полюса и нули передаточной функции усилителя, которые находятся в точках пересечения асимптот.
Как для инвертирующего, так и для неинвертирующего включения ОУ при резистивной обратной связи коэффициент передачи звена обратной связи определяется формулой
Согласно предыдущим выражениям, между и коэффициентом усиления входного сигнала К для схемы с идеальным ОУ существует следующая взаимосвязь:
В соответствии с
логарифмическим вариантом критерия
Найквиста для минимально-фазовых систем,
к которым можно отнести ОУ с отрицательной
обратной связью, усилитель будет
устойчив, если для логарифмических
частотных характеристик разомкнутой
петли обратной связи
выполнено условие
Для минимально-фазовых систем вид ЛАЧХ однозначно определяет вид ЛФЧХ. Поэтому для суждения об устойчивости усилителя достаточно иметь перед глазами только ЛАЧХ.
Для устойчивости усилителя с обратной связью необходимо и достаточно, чтобы точная ЛАЧХ петли регулирования пересекала ось частот с наклоном меньшим (по абсолютной величине), чем 40 дБ/дек.
При резистивной обратной связи ЛФЧХ петлевого усиления совпадает с ЛФЧХ усилителя, а ЛАЧХ петли проходит на 20lg(l/) ниже ЛАЧХ усилителя, так что частота среза fСР соответствует точке пересечения графика ЛАЧХ усилителя с горизонтальной прямой, проведенной на 20lg(l/) выше оси частот. На диаграмме видно, что при больших значениях К (и соответственно малых ) условие выполняется, причем имеется достаточный запас устойчивости по фазе. Однако, при К < 200 ОУс частотными характеристиками, такими, как на предыдущем рисунке, теряет устойчивость.
Степень устойчивости, а также мера затухания переходных процессов приближенно определяется запасом устойчивости по фазе . Под этой величиной понимается дополнительный до 180° угол к фазовому запаздыванию на критической частоте:
