2.3. Свойства операций над множествами

Множества, его подмножества и законы сочетания подмножеств образуют алгебраическую систему, которая называется булевой алгеброй.

1). Идемпотентность:

A  A = A,

A  A = A.

2). Коммутативность:

A  B = B  A,

A  B = B  A.

3). Ассоциативность:

A  (B  C) = (A  B)  C,

A  (B  C) = (A  B)  C.

4). Дистрибутивность:

A  (B  C) = (A  B)  (A  C),

A  (B  C) = (A  B)  (A  C).

5). Законы поглощения:

A  (A  B) = A,

A  (AB) = A.

6). Свойства нуля:

A   = A,

A   = ,

_.

7). Свойства единицы:

A  U = U,

A  U = A,

_.

8). Инволютивность:

_.

9). Законы де Моргана:

,

_.

10). Свойства дополнения:

,

.

2.4. Отображения множеств

Пусть X и Y - множества. Отображением f из множества X в множество Y мы будем называть правило, по которому каждому элементу х множества X ставится в соответствие вполне определенный (единственный) элемент y = f(x) множества Y. Обозначать данное отображение будем

f: X → Y.

Заметим, что отображение надо обязательно понимать как набор из трех элементов (X, Y, f), где X и Y - множества, f - закон.

Элемент множества Y, соответствующий при отображении f элементу x из X, обозначают f(x) и называют образом элемента x при этом отображении.

Если f(x) = y, то элемент x называют прообразом элемента y при отображении f.

Совокупность всех прообразов элемента y при отображении называется полным прообразом этого элемента и обозначается

f^-1 = {x: f(x) = y}.

Каждому подмножеству А множества Х (А  Х) соответствует его образ f(A) при отображении f. Этот образ состоит из всех элементов множества Y, которые являются образами какого-нибудь элемента из А:

f(A) = {y: y = f(a), a  A}.

Каждому подмножеству B множества Y (B  Y) соответствует его полный прообраз f^-1(В) при отображении f. Этот прообраз состоит из всех элементов, образы которых принадлежат В:

f^-1(В) = {x: f(x)  B}.

Множество А называется областью определения отображения f. Множество f(A) называется множеством значений этого отображения.

Отображение f : X → Y называется сюръективным, если для любого элемента у из множества Y существует непустой прообраз, то есть f^-1(y) ≠ Ø, т.е. каждый элемент множества Y имеет прообраз.

Отображение f : X → Y называется инъективным, если для любых x₁ ≠ x₂ из множества X следует, что f(x₁) ≠ f(x₂), т.е. для каждого элемента y существует не более одного прообраза.

Отображение f : X → Y называется биективным, если оно инъективно и сюръективно.

Примеры решения задач

1). Изобразить с помощью диаграмм Эйлера-Венна выражение

(А \ В)  (B \ A)

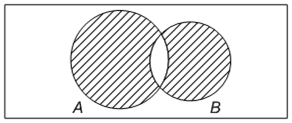
Изобразим два пересекающихся множества А и В:

Изобразим разность А \ В:

Изобразим разность В \ А:

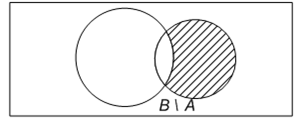
Изобразим объединение двух разностей:

2). Опрос 100 студентов о количестве студентов, изучающих иностранные языки, дал следующие результаты:

- испанский – 28,

- немецкий – 30,

- французский – 42,

- испанский и немецкий – 8,

- испанский и французский – 10,

- немецкий и французский – 5,

- все три языка – 3.

a). Сколько студентов не изучают ни одного языка?

b). Сколько студентов изучают один французский язык?

c). Сколько студентов изучает немецкий язык только в том случае, если они изучают еще и французский язык, но не изучают испанского.

Построим диаграмму Эйлера–Венна, изображающую множества студентов, изучающих различные языки:

Обозначим цифрами, сколько студентов приходится на каждую часть множества:

a). Все три языка – 3

b). Немецкий и французский учат всего 5, три из них учат еще и испанский, поэтому: 5 – 3 = 2.

c). Испанский и французский учат 10 студентов, из них 3 – еще и немецкий: 10 – 3 = 7.

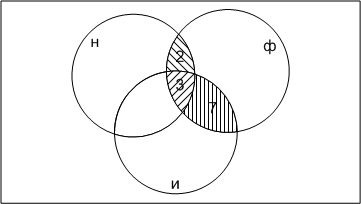
d). Немецкий и испанский учат 8, из них трое учат еще и французский, поэтому: 8 – 3 = 5.

e). только немецкий язык учат: 30 – 5 – 3 – 2 = 20, только французский: 42 – 2 – 3 – 7 = 30, только испанский: 28 – 5 – 7 – 3 = 13.

f). всего студентов, изучающих хотя бы один язык:

20 + 30 + 13 + 5 + 7 + 3 + 2 = 80,

тогда студентов, не изучающих ни одного языка: 100 – 80 = 20.