Упражнения

1). Составить таблицу истинности для логических выражений

1.1

1.2

1.3

1.4

1.5

1.6

1.7

1.8

1.9

1.10

2). Упростить логические выражения

2.1

2.2

2.3

2.4

2.5

2.6

2.7

2.8

2.9

2.10

3). Проверить эквивалентность формул

3.1

3.2

3.3

3.4

3.5

3.6

3.7

3.8

3.9

3.10

4). Выразить с помощью суперпозиций следующие функции. В случае невозможности выражения доказать это:

4.1

4.2

4.3

4.4

4.5

4.6

4.7

4.8

5). Привести формулу к КНФ

5.1

5.2

5.3

5.4

5.5

5.6

5.7

5.8

5.9

5.10

6). Привести формулу к СКНФ

6.1

6.2

6.3

6.4

6.5

6.6

6.7

6.8

6.9

6.10

7). Привести формулу к ДНФ

7.1

7.2

7.3

7.4

7.5

7.6

7.7

7.8

7.9

7.10

8). Привести формулу к СДНФ

8.1

8.2

8.3

8.4

8.5

8.6

8.7

8.8

8.9

8.10

9).Построить многочлен Жегалкина

9.1

9.2

9.3

9.4

9.5

9.6

9.7

9.8

9.9

9.10

10). Проверить линейность функции

10.1

10.2

10.3

10.4

10.5

10.6

10.7

10.8

10.9

10.10

Вопросы для самоконтроля и повторения

Что такое высказывание? Простое и составное высказывание.

1. Какими способами можно получить из простого высказывания составное? Что такое логические связки и какие они бывают?

2. Что такое таблица истинности?

3. Перечислите свойства логических операций.

4. Что такое функция алгебры логики и каковы ее свойства?

5. Как задаются функции одной и двух переменных?

6. Что такое нормальные формы, совершенные нормальные формы? Перечислите способы их построения.

7. Что такое полином Жегалкина и как он строится?

2. Множества и отображения

2.1. Множества

Множество - один из ключевых объектов математики, в частности, теории множеств и логики.

Понятие множества обычно принимается за одно из исходных (аксиоматических) понятий, то есть не сводимое к другим понятиям, а значит и не имеющее определения.

Объекты, из которых состоит множество, называют элементами множества или точками множества. Множества чаще всего обозначают большими буквами латинского алфавита, его элементы — маленькими. Если а – элемент множества А, то записывают а  А (а принадлежит А). Если а не является элементом множества А, то записывают а ∉ А (а не принадлежит А).

Если множество состоит из элементов a₁, a₂,… a_n, то пишут a₁, a₂,… a_n  А или А = { a₁, a₂,… a_n}. При этом порядок перечисления элементов значения не имеет.

Множество A является подмножеством множества B, если любой элемент, принадлежащий A, также принадлежит B, пишут A  B. Множество B в таком случае называется надмножеством множества A, и этот факт часто записывают: B  A.

Множества, содержащие в качестве элементов другие множества, называются семействами или классами.

Множества, не содержащие ни одного элемента, называются пустыми и обозначаются . Множества, содержащие один элемент – единичные множества.

2.2. Операции над множествами.

Что бы представить операции над множествами, можно пользоваться диаграммами Эйлера-Венна. Прямоугольник здесь обозначает универсальное множество, а круги – его подмножества (рис. 1.1).

Рис. 1.1	Рис. 1.2

1). Дополнением к множеству А называется множество элементов, которые не содержатся в А. Обозначается ₍рис. 1.2₎.

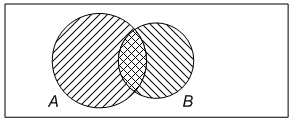
2). Пересечением множеств А и В называется множество элементов, принадлежащих и А и В. Обозначается А  В (рис. 1.3).

Рис. 1.3	Рис. 1.4

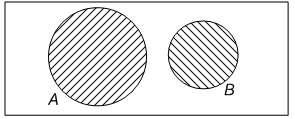
Если А и В ­– непустые множества, пересечение которых пусто, т.е. А  В = , то их называют непересекающимися (рис. 1.4).

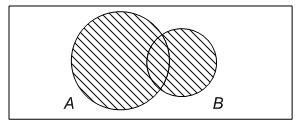
3). Объединением множеств А и В называется множество элементов, принадлежащих либо А либо В либо обоим. Обозначается А  В (рис. 1.5).

Рис. 1.5	Рис.1.6

4). Разностью множеств А и В называется множество элементов, принадлежащих А, но не принадлежащих В. Обозначают А \ В (рис. 1.6).