Примеры решения задач

1). По таблицам Милли и Мура найти выходное слово при входном слове x₁x₂x₂x₂x₁

Таблица 6.3

Автомат Мили					Автомат Мура
xj\ai	a0	a1	a2	a3	yg	y2	y1	y1	y3	y2
x1	a1/y1	a2/y3	a3/y2	a0/y1	xj/ xj	a0	a1	a2	a3	a4
x2	a0/y2	a0/y1	a3/y1	a2/y3	x1	a2	a1	a3	a4	a2
					x2	a3	a4	a4	a0	a1

Для автомата Милли:

a). Изначально автомат находится в состоянии a₀. При поступлении на вход первого символа x₁ автомат перейдет в состояние a₁ и на выходе будет символ y₁.

b). При поступлении на вход второго символа x₂ автомат находится уже в состоянии a₁, состояние изменится на a₀, а на выходе получим y₁, и т.д.

c). На выходе получим слово y₁y₁y₂y₂y₁.

Для автомата Мура:

a). Изначально автомат находится в состоянии a₀. При поступлении на вход первого символа x₁ автомат перейдет в состояние a₂ и на выходе будет символ y₂.

b). При поступлении на вход второго символа x₂ автомат находится уже в состоянии a₂, состояние изменится на a₄, а на выходе получим y₁, и т.д.

c). На выходе получим слово y₂y₁y₂y₁y₂.

2). Для приведенных в примере 1) таблиц Милли и Мура построить графы для задания автоматов.

Для автомата Милли:

a). Нарисуем четыре вершины графа, каждая из которых соответствует одному из состояний автомата.

b). Соединим две вершины, если есть переход между соответствующими состояниями. Над ребрами напишем через дробь входной и выходной сигнал.

Рис. 6.1

Для автомата Мура:

a). Нарисуем пять вершин графа, каждая из которых соответствует одному из состояний автомата. Через дробь к состоянию припишем соответствующее значение выходного сигнала.

b). Соединим две вершины, если есть переход между соответствующими состояниями. Над ребрами напишем входной сигнал.

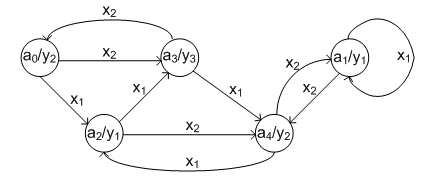
Рис. 6.2

3). Представить в виде конечного автомата элемент задержки.

Решение

Элемент задержки представляет собой устройство, имеющее один вход и один выход, причем, значение выходного сигнала в момент времени t совпадает со значением сигнала в предыдущий момент времени. Схематично элемент задержки изобразим следующим образом:

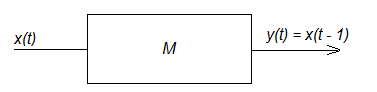
Рис. 6.3

Предположим, что входной, и, следовательно, выходной алфавит есть: X{0,1}, Y{0,1}. Кроме того, А{0,1} – под состоянием элемента задержки в момент времени t понимается содержание элемента памяти в данный момент. Таким образом, а(t) = X(t – 1), Y(t) = а(t) = X(t – 1).

Зададим элемент задержки таблицей, где х₁ = 0, х₂ = 1, а₁ = 0, а₂ = 1.

 (x₁; a₁) =  (0; 0) = 0  (x₁; a₁) =  (0; 0) = 0

 (x₁; a₂) =  (0; 1) = 0  (x₁; a₂) =  (0; 1) = 1

 (x₂; a₁) =  (1; 0) = 1  (x₂; a₁) =  (1; 0) = 0

 (x₂; a₂) =  (1; 1) = 1  (x₂; a₂) =  (1; 1) = 1

Таблица 6.4

x\a	0	1
0	 = 0,  = 0	 = 0,  = 1
1	 = 1,  = 0	 = 1,  = 1

Для представления этого автомата системой булевых функций используем таблицу автомата: находим числа k, r, s, удовлетворяющие условиям:

2^k-1 < m < 2^k,

2^r-1 < n < 2^r,

2^s-1 < p < 2^s,

где m = 2, n = 2, p = 2 - число символов множеств.

При этом видно, что k, r, s равны числу разрядов, в двоичном представлении чисел m, n, p: k = 1, r = 1, s = 1, k + r + r + s = 4, т.о. таблица истинности содержит четыре строки.

Таблица 6.5

x	y		
0	0	0	0
0	1	0	1
1	0	1	0
1	1	1	1

4). Представить в виде конечного автомата двоичный сумматор последовательного действия.

Решение

Данный сумматор представляет собой устройство, осуществляющее сложение двух чисел в двоичной системе исчисления. На входы сумматора подаются числа х₁ и х₂, начиная с младших разрядов. На выходе формируется последовательность, соответствующая записи числа х₁ + х₂ в двоичной системе исчисления.

Рис. 6.4

Входной и выходной алфавит заданы однозначно: Х = {00, 01, 10, 11}, Y = {0, 1}. Множество состояний определяется значением переноса при сложении соответствующих разрядов чисел х₁ и х₂. Если при сложении некоторых разрядов образовался перенос, то будем считать, что сумматор перешел в состояние a₁. При отсутствии переноса будем считать, что сумматор находится в состоянии a₀.

Сумматор задается таблицей (если состояние а₀, то при комбинациях 00, 01, 10 – сумма будет 0 или 1, при 11 – сумма равна 10, есть перенос – состояние меняется на а₁; если состояние а₁ – то подразумеваем, что прошлым действием был перенос и 1 держим «в уме», теперь при сложении 00 будет на выходе 1 (с учетом 1 «в уме»), следующее состояние а₀ – переноса не было, при сложении 01 или 10, то с учетом единицы в уме получаем 10, наблюдаем перенос и состояние устанавливаем в а₁, на выходе 0, при сложении 11, то с учетом единицы в уме получаем 11, наблюдаем перенос и состояние устанавливаем в а₁, на выходе 1):

Таблица 6.6

х\а	a0	a1	текущее состояние
00	a0; 0	a0; 1	следующее состояние; выход
01	a0; 1	a1; 0
10	a0; 1	a1; 0
11	a1; 0	a1; 1