Алгоритм Дейкстры-Прима

a. Нарисуем города – вершины графа, найдем число необходимых ребер: 6-1 = 5
b. Выберем ребра, имеющие минимальный вес 1: 1-4, 2-5, 4-5, включаем их в граф
c. Опять выберем ребра с минимальным весом 2: 1-3, 1-6, 3-5, ребро 3-5 образует цикл, поэтому в граф его включать не будем. Т.к. количество ребер равно 5, то минимальное остовное дерево построено.

Вес минимального остовного дерева равен: 1 + 1 + 1 + 2 + 2 = 7.

3) Найти кратчайшие пути от вершины 1 до всех остальных вершин графа, изображенного на рис. 4.16, по алгоритму Дейкстры.

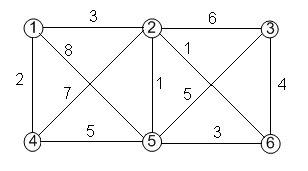
Рис. 4.16

Решение:

a) Т.к. исходная вершина 1, то длина пути 1-1 = 0 – постоянная метка (обозначили +). всем остальным вершинам присвоим метки .

Таблица 4.2

1	2	3	4	5	6	рассматриваемая вершина
0+						p = 1

b) Из вершины 1 выходят дуги в вершины 2, 4, 5. Пересчитываем метки этих вершин и заполняем следующую строку:

d(2) = min (; 0 + 3) = 3

d (4) = min (; 0 + 2) = 2

d (5) = min (; 0 + 8) = 8

В качестве постоянной выберем вершину с меньшей меткой 2 – вершина 4.

Таблица 4.3

1	2	3	4	5	6	выбранная вершина
0+						p = 1
0+	3		2+	8		p = 4

c) Из вершины 4 выходят дуги в вершины 2, 5. Пересчитываем метки этих вершин и заполняем следующую строку:

d (2) = min (3; 2 + 7) = 3

d (5) = min (8; 2 + 5) = 7

В качестве постоянной выберем вершину с меньшей меткой 3 – вершина 2.

Таблица 4.4

1	2	3	4	5	6	выбранная вершина
0+						p = 1
0+	3		2+	8		p = 4
0+	3+		2+	7		p = 2

d) Из вершины 2 выходят дуги в вершины 3, 5, 6. Пересчитываем метки этих вершин и заполняем следующую строку:

d (3) = min (; 3 + 6) = 9

d (5) = min (7; 3 + 1) = 4

d (6) = min (; 3 + 1) = 4

Так как метки вершин 5 и 6 одинаковы, то в качестве постоянной вершину выберем произвольно – вершина 5.

Таблица 4.5

1	2	3	4	5	6	выбранная вершина
0+						p = 1
0+	3		2+	8		p = 4
0+	3+		2+	7		p = 2
0+	3+	9	2+	4+	4	p = 5

e) Из вершины 5 выходят дуги в вершины 3, 6. Пересчитываем метки этих вершин и заполняем следующую строку:

d (3) = min (9; 4 + 5) = 9

d (6) = min (4; 4 + 3) = 4

В качестве постоянной выберем вершину с меньшей меткой 4 – вершина 6.

Таблица 4.6

1	2	3	4	5	6	выбранная вершина
0+						p = 1
0+	3		2+	8		p = 4
0+	3+		2+	7		p = 2
0+	3+	9	2+	4+	4	p = 5
0+	3+	9	2+	4+	4+	p = 6

f) Из вершины 6 выходит дуга в вершину 3. Пересчитываем метку этой вершины и заполняем последнюю строку:

d (3) = min (9; 4 + 4) = 8

В качестве постоянной выберем вершину с меньшей меткой 8 – вершина 3. На этом расчет окончен, найдены кратчайшие пути до всех вершин графа из точки 1.

Таблица 4.7

1	2	3	4	5	6	выбранная вершина
0+						p = 1
0+	3		2+	8		p = 4
0+	3+		2+	7		p = 2
0+	3+	9	2+	4+	4	p = 5
0+	3+	9	2+	4+	4+	p = 6
0+	3+	8+	2+	4+	4+	p = 3

4) Определить кратчайшие пути от вершины 1 до всех остальных вершин графа, изображенного на рис. 4.17, по алгоритму Беллмана.

a). Для построения кратчайших путей графа удобно воспользоваться таблицей: в столбцах записаны вершины графа, в строках - . Первый столбец соответствует первой вершине s и содержит только 0.

Рис. 4.17

b). На первом шаге находятся пути одной дуги от вершины 1 до вершин 2,4,5.

c). Занесем в строку 1, если пути нет, то ставим . Пути состоящие более чем из 2-х дуг следует искать только для вершин, в которые входят дуги, выходящие из вершин 2,4,5:

из 2 – в 3,4,5,6

из 4 – в 2,5,7,8

из 5 – в 2,3,4,6,7,9

d). Уменьшились длины путей до вершин: 2,3,6,7,8,9. А значит, имеет смысл искать более короткие дуги до тех вершин графа, в которые входят дуги из перечисленных вершин

из 2 – в 3,4,5,6

из 3 – в 2,5,6

из 6 – в 3,5,8,9

из 7 – в 4,5,8

из 8 – в 4,5,6,7,9

из 9 – в 5,6

_.

e). Уменьшились длины путей до вершин: 3,5,6,8,9. А значит, имеет смысл искать более короткие дуги до тех вершин графа, в которые входят дуги из перечисленных вершин. И т.д.

f). При заполнении 7-й строки обнаруживаем, что значения строки повторяют 6-ю строку, а значит, алгоритм закончил свою работу.

Составим дерево кратчайших путей:

- корень – вершина 1

- длина кратчайшего пути до вершины 4 была найдена уже на первом шаге – включаем дугу 1-4 в дерево.

- во второй строке стоят кратчайшие пути до вершин 2 и 7, а из диаграммы видно, что эти пути идут через вершину 4.

- в третьей строке стоит кратчайший путь до вершины 6 (содержит три дуги), а из диаграммы видно, что этот пути идет через вершины 4 и 2, и т.д.

Таблица 4.8

	1	2	3	4	5	6	7	8	9
1	0	6		2	7				
2	0	5	9	2	7	2	3	8	13
3	0	5	7	2	5	1	3	3	6
4	0	5	6	2	2	1	3	2	1
5	0	5	4	2	1	1	3	2	0
6	0	5	3	2	1	1	3	2	0
7	0	5	3	2	1	1	3	2	0

Дерево:

Рис. 4.18

5) Отыскать все гамильтоновы циклы графа, изображенного на рис. 4.19.

Рис. 4.19

Решение:

a). Выберем вершину 1 за начальную точку.

b). Выпишем наборы, состоящие из начальной вершины и смежной с ней: 1-2, 1-3, 1-4.

c). Выпишем наборы, состоящие из наборов п. 2 и смежных с ними вершин: 1-2-5, 1-3-4, 1-3-5, 1-4-3, 1-4-5.

d). Выпишем наборы, состоящие из наборов п. 3 и смежных с ними вершин: 1-2-5-3, 1-2-5-4, 1-3-4-5, 1-3-5-4, 1-3-5-2, 1-4-3-5, 1-4-5-3, 1-4-5-2.

e). Выпишем наборы, состоящие из наборов п. 4 и смежных с ними вершин: 1-2-5-3-4, 1-2-5-4-3, 1-3-4-5-2, 1-3-5-4, 1-3-5-2, 1-4-3-5-2, 1-4-5-3, 1-4-5-2, наборы 1-3-5-4, 1-3-5-2, 1-4-5-3, 1-4-5-2 не включают пятую вершину, а значит, не образуют гамильтонова цикла.

f). Замкнем цикл - 1-2-5-3-4-1, 1-2-5-4-3-1, 1-3-4-5-2-1, 1-4-3-5-2-1.

Рис. 4.20 – Дерево гамильтоновых циклов

6) Проверить является ли граф, изображенный на рис. 4.21, эйлеровым, полуэйлеровым или не эйлеровым, в первых двух случаях построить эйлеров цикл или эйлеров путь соответственно.

Рис. 4.21

Решение:

По теореме Эйлера проверим четность степеней вершин графа (посчитаем количество вершин, смежных с данной):

Все степени вершин являются четными (таблица 4.9), значит, граф является эйлеровым. Отыщем эйлеров цикл в графе по алгоритму Флёри, за начало пути возьмем вершину 1.

Таблица 4.9

Вершина	Степень вершины
1	2
2	4
3	2
4	4
5	4
6	2
7	2

1) Убираем ребро 1-2 2) Убираем ребро 2-3

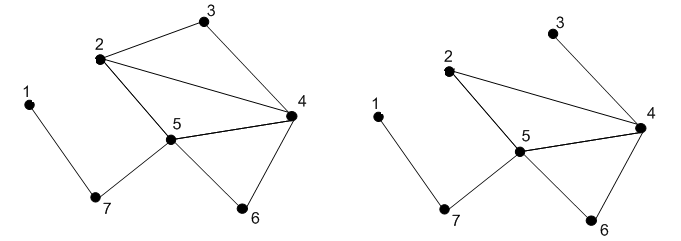
3) Убираем ребро 3-4 и вершину 3 4) Убираем ребро 4-6

5) Убираем ребро 6-5 и вершину 6 6) Убираем ребро 5-4

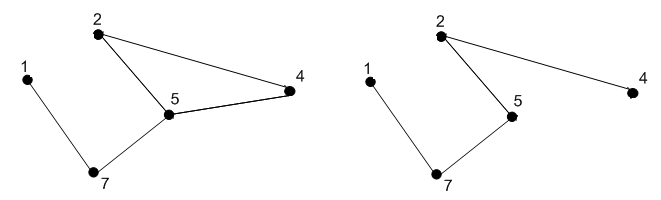
7) Убираем ребро 4-2 и вершину 4 8) Убираем ребро 2-5

9) Убираем ребро 5-7 и вершину 5, вернулись в исходную вершину 1.

10) Эйлеров цикл: 1-2-3-4-6-5-4-2-5-7-1 – граф – эйлеров.