4.4. Мосты, деревья

При удалении ребра e(v₁-v₂) из графа G получается граф с теми же вершинами, что и граф G, и всеми ребрами, кроме ребра e(v₁-v₂). При удалении ребра из связного графа новый граф может оказаться как связным, так и несвязным.

Ребро e(v₁-v₂) называется мостом графа G, если в графе, полученном после удаления из G ребра e(v₁-v₂), вершины v₁ и v₂ оказываются несвязными. Существует несколько признаков мостов (рис. 4.10):

1). Ребро e(v₁-v₂) является мостом в том и только в том случае, если e - единственный путь, соединяющий вершины v₁ и v₂ (вершины 1 и 2).

2). Ребро e(v₁-v₂) является мостом в том и только в том случае, если найдутся две вершины v₃ и v₄, такие, что каждый путь, соединяющий их, содержит v₁ и v₂. (путь из точки 11 в точку 8 обязательно идет через ребро 1-2).

3). Ребро e(v₁-v₂) является мостом в том и только в том случае, если оно не принадлежит ни одному циклу (ребро 9-10 принадлежит циклам, 1-2 – не принадлежит).

Рис. 4.10

Деревом называется связный граф, не имеющий циклов. В графе без циклов, таким образом, каждая компонента связности является деревом. Такой граф называют лесом.

Для дерева характерны следующие понятия:

- корневой узел — самый верхний узел дерева.

- корень — одна из вершин, по желанию наблюдателя.

- листовой узел или лист — узел самого нижнего уровня дерева.

- листья дерева — корни, из которых не выходит ни одной дуги.

- внутренний узел — любой узел дерева, имеющий потомков, и таким образом не являющийся листовым узлом.

Дерево считается ориентированным, если в корень не заходит ни одно ребро (рис. 4.11).

Граф с n вершинами и m ребрами является деревом тогда и только тогда, когда он удовлетворяет любым двум из следующих трех условий:

1) связен;

2) не имеет циклов;

3) m = n-1.

Рис. 4.11 – Ориентированное дерево, вершина 1 – корень.

Если G - дерево, то:

1) в G любая пара вершин соединена единственным путем;

2) при добавлении к G любого нового ребра образуется цикл;

3) при удалении из G любого ребра он превращается в несвязный граф.

Корневые деревья: часто в дереве особо выделяется одна вершина, играющая роль своего рода "начала отсчета". Дерево с выделенной вершиной называют корневым деревом, а саму эту вершину - корнем. Из дерева с n вершинами можно, таким образом, образовать n различных корневых деревьев.

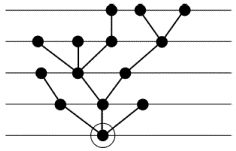
Рис. 4.12

При графическом изображении корневого дерева обычно придерживаются какого-нибудь стандарта. Один из наиболее распространенных состоит в следующем. Возьмем на плоскости семейство параллельных прямых с равными расстояниями между соседними прямыми. Изобразим корень точкой на одной из этих прямых, смежные с корнем вершины - точками на соседней прямой, вершины, находящиеся на расстоянии 2 от корня, - на следующей, и т.д. Ребра изобразим отрезками прямых. Ясно, что вершины на каждой прямой можно разместить так, чтобы ребра не пересекались. Пример нарисованного таким образом корневого дерева показан на рис. 4.12 (корень обведен кружком). Чаще дерево рисуют корнем вверх, а не вниз.

Иногда бывает полезно ребра корневого дерева ориентировать так, чтобы в каждую вершину вел ориентированный путь из корня (для дерева на рис. 4.12 это означает, что каждое ребро ориентируется снизу вверх). Такое ориентированное корневое дерево будем называть исходящим деревом. В исходящем дереве каждая вершина, кроме корня, является концом единственного ребра. Если в исходящем дереве имеется ребро e, то вершину v₁ называют отцом вершины e, а вершину v₂ - сыном вершины e. Естественный и для многих целей удобный способ задания корневого дерева состоит в указании для каждой вершины ее отца. При этом иногда считают, что корень приходится отцом самому себе - это равносильно добавлению петли при корне.

Если в исходящем дереве имеется ориентированный путь из вершины v1 в вершину v₂, то говорят, что v₁ - предок v₂, а v₂ - потомок v₁. В частности, каждая вершина является предком и потомком самой себя. Множество всех предков вершины v_n порождает ориентированный путь из корня в v_n. Множество всех потомков вершины v₁ порождает исходящее дерево с корнем в v₁, оно называется ветвью дерева G в вершине v₁.

Высота узла — это максимальная длина нисходящего пути от этого узла к самому нижнему узлу (краевому узлу), называемому листом. Высота корневого узла равна высоте всего дерева. Глубина вложенности узла равна длине пути до корневого узла

Высота корневого дерева - это максимальное количество дуг, отделяющих листья от корня. Если дерево не взвешенное, то его высота - это просто расстояние от корня до самого удаленного листа.

Остовное дерево связного неориентированного графа — ациклический связный подграф данного графа, в который входят все его вершины.

Если каждому ребру e(v₁, v₂) графа G поставлено в соответствие положительное число w(e), то говорят, что у ребра есть вес.

Весом остовного дерева называют сумму весов ребер, составляющих это дерево. Минимальное остовное дерево (или минимальное покрывающее дерево) в связанном, взвешенном, неориентированном графе — это остовное дерево этого графа, имеющее минимальный возможный вес. Существует несколько алгоритмов для нахождения минимального остовного дерева. Некоторые наиболее известные из них перечислены ниже:

- Алгоритм Дейкстры-Прима;

- Алгоритм Краскала (или алгоритм Крускала);

- Алгоритм Борувки.