4.2. Основные операции над графами

В ряде задач теории графов используются двуместные операции над графами:

1). Дополнением графа G₁(V₁, E₁) называется граф , множеством вершин которого является множество V₁, а множеством его ребер является множество

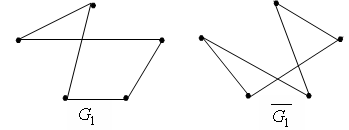
Рис. 4.5

2). Объединением графов G₁(V₁, E₁) и G₂(V₂, E₂) называется граф G₁(V₁, E₁)  G₂(V₂, E₂), множество вершин которого есть объединение множеств вершин графов G₁ и G₂ V = V₁  V₂, а множество ребер является объединением множеств ребер этих графов E = E₁  E₂.

3). Пересечением графов G₁(V₁, E₁) и G₂(V₂, E₂) называется граф G₁(V₁, E₁)  G₂(V₂, E₂), множество вершин которого есть множество V = V₁  V₂, а множество ребер является множество E = E₁  E₂. (только те ребра, и вершины, которые принадлежат обоим графам).

4). Суммой по модулю два графов G₁(V₁, E₁) и G₂(V₂, E₂) называется граф G₁(V₁,E₁)  G₂(V₂,E₂), порожденный на множестве ребер , т.е. на множестве ребер, присутствующих либо в G₁, либо в G₂, но не принадлежащих их пересечению E = E₁  E₂.

5). Простейшая операция - удаление ребра. При удалении ребра сохраняются все вершины графа и все его ребра, кроме удаляемого. Обратная операция - добавление ребра.

6). При удалении вершины вместе с вершиной удаляются и все инцидентные ей ребра. Граф, получаемый из графа G удалением вершины v, обозначают G-v. При добавлении вершины к графу добавляется новая изолированная вершина. С помощью операций добавления вершин и ребер можно "из ничего", то есть из графа G, построить любой граф.

Рис. 4.6

7). Операция стягивания ребра E определяется следующим образом. Вершины v₁ и v₂ удаляются из графа, к нему добавляется новая вершина v₃ и она соединяется ребром с каждой вершиной, с которой была смежна хотя бы одна из вершин v₁ и v₂ (рис. 4.7, 2).

8). Операция подразбиения ребра e действует следующим образом. Из графа удаляется это ребро, к нему добавляется новая вершина v₁ и два новых ребра e₁ и e₂ (рис. 4.7, 3).

1) 2) 3)

Рис. 4.7

4.3. Матрицы графов

Матрица смежности графа G с конечным числом вершин n (пронумерованных числами от 1 до n) — это квадратная матрица A размера n, в которой значение элемента a_ij равно числу ребёр из i-й вершины графа в j-ю вершину. Матрица смежности простого графа (не содержащего петель и кратных ребер) является бинарной матрицей и содержит нули на главной диагонали.

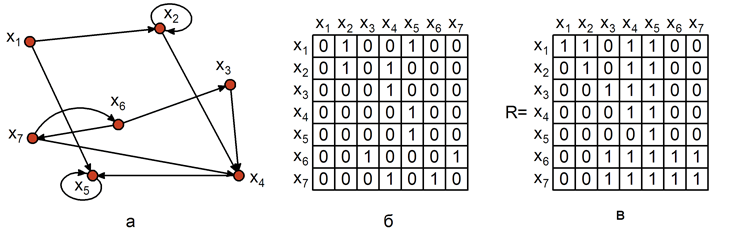
Рис. 4.8 – Граф, матрица смежности (б), матрица достижимости (в) графа

Достижимость в графе описывается матрицей достижимости

R = [r_ij],

i, j = 1, 2, ... n, где n – число вершин графа, а каждый элемент определяется следующим образом:

r_ij = 1, если вершина v_j достижима из v_i ,

r_ij=0, в противном случае.

Множество вершин R(v_i) графа G, достижимых из заданной вершины v_i, состоит из таких элементов v_i, для которых (i, j)-й элемент в матрице достижимостей равен 1.

Матрица инциденций представляет собой прямоугольную матрицу размером n x m, где n – количество вершин графа, а m – количество дуг графа. Обозначается матрица инциденций B = {b_ij}, i = 1, 2, ..., n, j = 1, 2, ..., m.

Каждый элемент матрицы определяется следующим образом:

b_ij = 1, если v_i является начальной вершиной дуги e_j,

b_ij = –1, если v_i является конечной вершиной дуги e_j,

b_ij = 0, если v_i не является концевой вершиной дуги e_j или если e_j является петлей.

Рис. 4.9 – Граф и его матрица инциденций

Для неориентированного графа, матрица инциденций определяется так же, за исключением того, что все элементы, равные –1, заменяются на 1.