95

Тема 3. Введение в анализ. Дифференциальное исчисление функции одной переменной Программный объем темы

1. Предел, непрерывность функции, основные свойства пределов, бесконечно малые и бесконечно большие. Замечательные пределы. Сравнение бесконечно малых. Эквивалентные бесконечно малые. Вы­числение пределов с различными видами неопределенностей.

2. Определение производной, ее геометрический и механический смысл. Непрерывность и дифференцируемость. Основные правила нахо­ждения производных. Дифференциал функции. Производные и диффе­ренциалы высших порядков.

3. Применение пределов и производных к исследованию функций и построению их графиков. Правило Лопиталя и его применение к вычис­лению пределов.

3.1. Введение в анализ

Пусть функция f(x) определена в окрестности некоторой точки х=а, за исключением, быть может, самой точки а.

Определение (на языке « »). Число А называется пределом функции f(x) при , если для любого >0 можно указать такое >0, что для всех х, удовлетворяющих соотношениям , имеет место неравенство .

Тот факт, что А есть предел f(х) при , записывают в виде .

Если х<а (х>а) и , то пишут –0 ( +0). В первом случае говорят, что X стремится к а слева, во втором случае – справа.

Определение (на языке « »). Число A называется пределом функции f(х) при –0, если для любого > 0 найдется такое > 0, что для всех X, удовлетворяющих соотношениям , имеет место неравенство .

Аналогично определяется предел функции f(х) при справа. Тот факт, что функция f(х) при слева и справа имеет своими пределами числа А_– и A₊; записывают в виде , .

Данные пределы обозначают также символами f(а–0), f(а+0).

Пусть функция f(х) определена для всех х, достаточно больших по абсолютной величине ( ).

Определение (на языке « »). Число А называется пределом функции f(x) при , если для любого >0 можно указать число М (М>К), такое, что для всех |х| > М выполняется неравенство .

Обозначение: . Подобным образом вводятся пределы при , .

По аналогии со случаями конечных пределов (А - конечно) можно ввести пределы:

, ,

, ,

, .

Например, обозначает, что при любом заданном отрицательном числе N существует такое число M>0, что f(x)<N, если x>M.

Основные свойства пределов.

Пусть , , где А и В - конечные числа.

Тогда

1. ,

2. ,

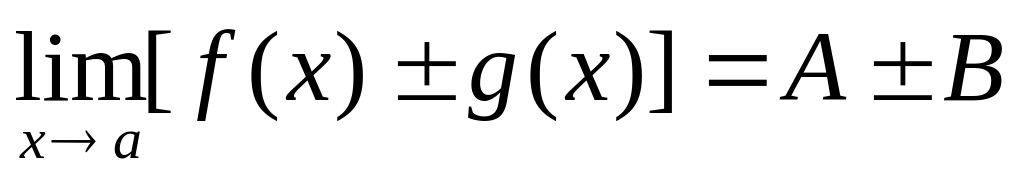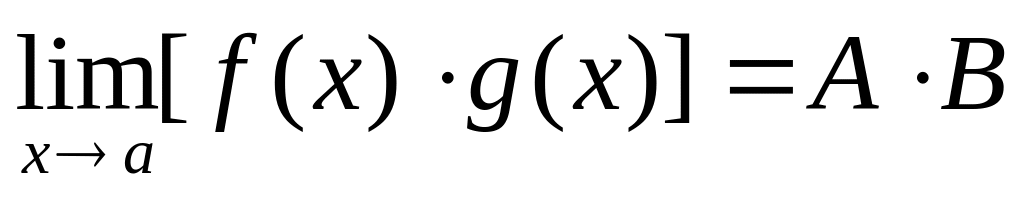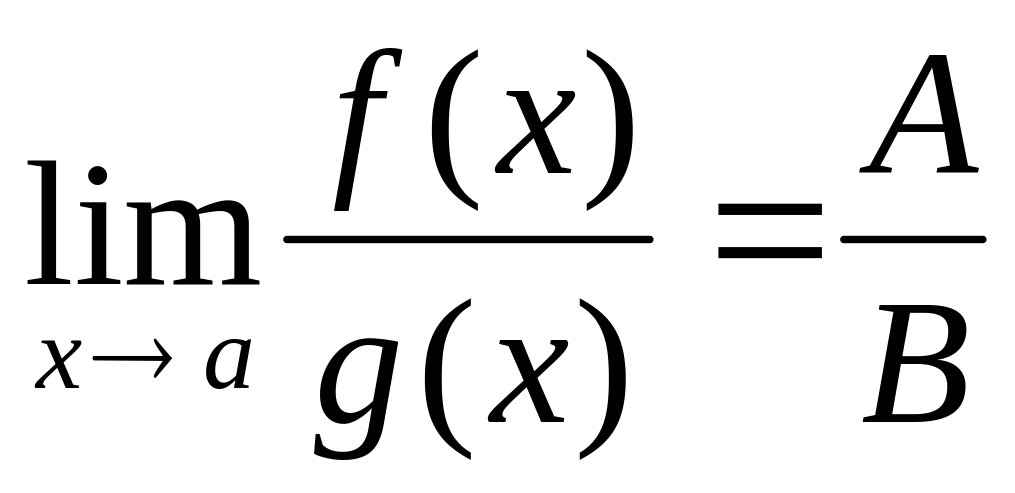3. (при условии, что ).

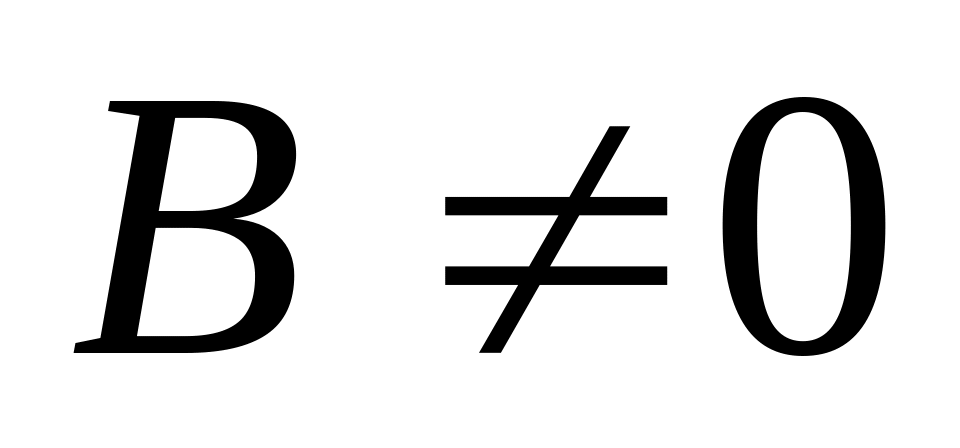При решении задач полезно помнить таблицу простейших пределов:

, ,

, ,

, ,

, ,

, .

В таблице а>0, .

Технически проще всего находится предел элементарной функции f(x) при , если x₀ принадлежит области определения этой функции. Такой предел равен f(x₀). Ниже приведены основные поло­жения, объясняющие этот результат.

Определение. Класс функций, включающий в себя многочлены, рациональные функции, показательные, степенные, логарифмические, тригонометрические и обратные тригонометрические функции, а также функции, получающиеся из перечисленных с помощью четырех арифме­тических действий и суперпозиций (образование сложной функции), примененных конечное число раз, называют элементарными функция­ми.

Например, , , , y=tglncos³x² принадлежат к классу элементарных функций.

Теорема. Любая элементарная функция непрерывна в каждой точке своей области определения.

Теорема. Под знаком непрерывной в данной точке Х₀ функции f(х) возможен предельный переход в этой точке: .