If the blade section area decreases from the root to periphery under the linear law:

^(3.10)

than integration by formula (3.7) will result in:

(3.11)

where h=R₀-R_r is the length of blade airfoil part.

The maximum stress takes place in the blade root and is calculated by the formula

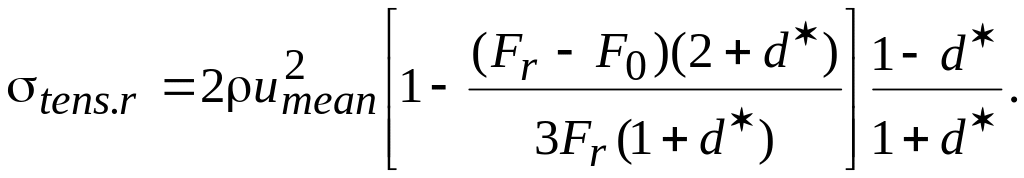(3.12)

We can see from the formula (3.12), that the considerable stress reduction can be reached if area ratio F₀/F_r is decreased. In modern compressor rotor blades F₀/F_r=0,25...0,35, which permits along with other equal terms to reduce stress in blade root by 30...35 % compared with stresses in the constant area blades.

The blade section area changes according to the exponential law

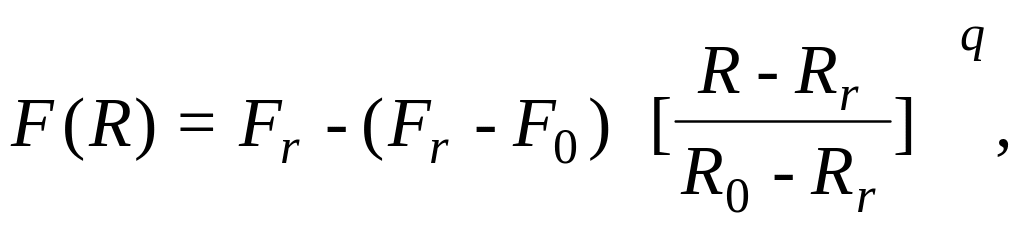(3.13)

where q is an exponent (q=0,5...0,6 for turbine blades; q=1 for compressor blades).

In this case an integration by formula (3.7) yields

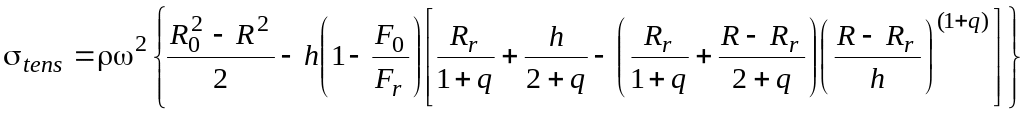
(3.14)

For the blade root from the formula (3.14) we will have

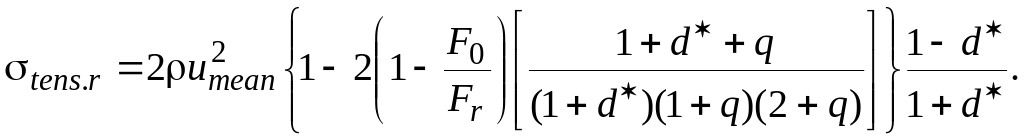(3.15)

As it follows from the formula (3.15), the exponent q decreasing from 1 to 0 results in a considerable stress reduction in the blade root as compared with the law of linear areas changing. In this case the maximum of stress moves from blade root to mean section that may result in underloading of turbine rotor blades root. Therefore, it is necessary to optimize selection of an exponent q. At optimal values of q and F₀/F_r the tensile stress in the blade root can be reduced by 40...45 % in comparison with version F=const.

If the blade section area changes according to arbitrary law, then the approximate integration by formula (3.7) should be done to define stresses, for example, by Simpson’s rule. In this case we will get the following recurrence formula:

(3.16)

where i=2,4,6... are even numbers of design sections; n is the number of all sections, which should be even.

The maximum values of tensile stresses by centrifugal forces in axial compressors reach 300...350 MPa for steel blades, 100...150 MPa for blades from aluminium‑based alloys and 200...250 MPa for blades from titanium‑based alloys. The maximum tensile stresses can reach the values of 250...300 MPa in gas-turbine rotor blades, though in actual designs they seldom exceed 200 MPa.

3. Determination of rotor blade bending stress caused by gas forces

The geometry of rotor blades airfoils or blade attachment to the disc are designed so that the bending momenta, caused by gas and centrifugal forces, have opposite directions. Therefore the full or partial blade bending stress unloading will be provided. It is necessary to analyze the blade bending stress, caused by gas and centrifugal forces separately, to perform in the right way.

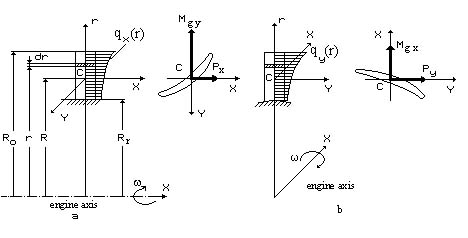
Fig. 3.2. Design scheme of turbine rotor blade loading with gas forces

in axial (a) and circumferential (b) planes

3.3.1. Design scheme of a blade

The gas force is distributed along an airfoil center-of-pressure line and affects the blade. It is characterized by load intensity in an axial plane q_x and in a plane of rotation q_y (Fig. 3.2). Load intensity is the force which acts on the blade length unit. Generally gas load intensity is distributed along radius according to the arbitrary law. Nevertheless it can be accepted as a constant value along the blade airfoil part when roughly calculated.

Let us consider a blade as an asymmetrical section rod with arbitrary variation of a section area along its length. A blade is considered rigidly nipped in the disc with the blade bending about this disc.

In arbitrary section of a blade at the radius r (see Fig. 3.2) we will place local (rotating) coordinate system xCy. We will arrange origin C in the center of gravity of the section under consideration (x axis is directed towards the gas flow movement, and y axis – along the tangent to a circle of R radius towards the rotor rotation). We will consider the intensities of gas loads positive, if their vectors coincide with directions of x and y axes.

Vectors of the bending momenta, coming into action in an axial plane (M_{g y}) and a plane of rotation (M_{g x}), will be guided along x and y axes, always in positive direction.

According to the design scheme considered, the problem of blade bending calculation is reduced to the problem of asymmetrical section beam skew bending.