6 Определение параметров проектного профиля

Ввиду того, что проектный забой бокового ствола имеет большое смещение от точки забуривания. Требуется использовать проектный профиль бокового ствола 2-го типа.

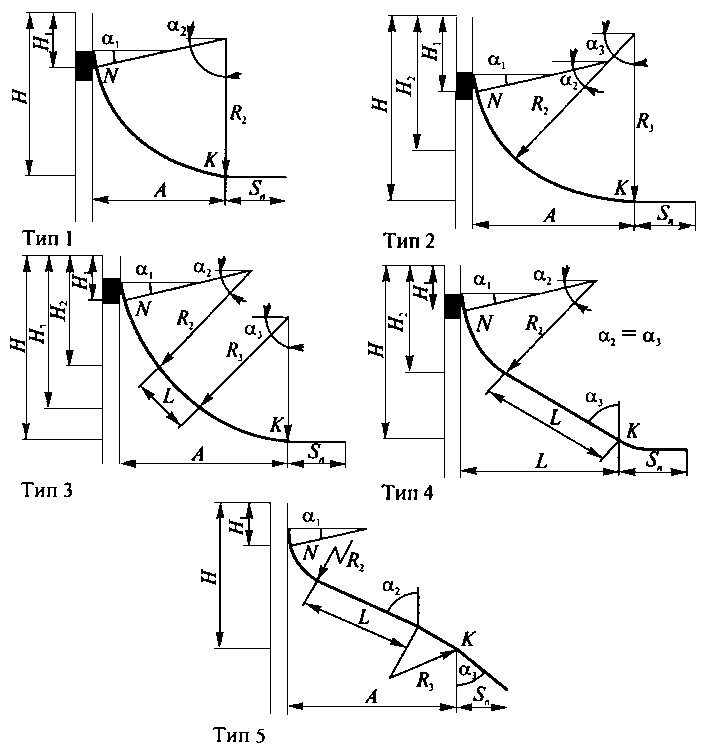
Параметры проектного профиля, определяются совместным решением следующих двух уравнений:

Н - Н - R #S (sin - sin ) - R (sin - sin ) = 0

А - R #S (cos - cos ) - R (cos - cos ) = 0 (10)

где H – глубина по вертикали от устья скважины до точки К в продуктивном пласте, м;

H₁ – глубина по вертикали от устья скважины до точки забуривания бокового ствола, м;

α₁ – зенитный угол скважины в начальной точке забуривания бокового ствола, град (α₁ принимается равным углу скоса клина – отклонителя);

α₂ – зенитный угол скважины в конечной точке забуривания бокового ствола, град;

α₃ – зенитный угол скважины в точке К, град;

R₂ – радиус кривизны участка забуривания бокового ствола, м;

R₃ – радиус кривизны участка изменения зенитного угла бокового ствола, м ;

А – смещение бокового ствола скважины от начальной точки забуривания, м.

Из системы уравнений (10) необходимо определить следующие параметры: L и R₃. Остальные параметры даны в исходных данных, либо были определен ранее.

Зенитный угол скважины в точке К примем равным =90°

Н - Н - R #S (sin - sin ) - R (sin - sin ) = 0

1900-1520-200(sin45° - sin2,5°)- R₃·(sin – sin45°)=0

А - R #S (cos - cos ) - R (cos - cos ) = 0

800-340,4·(cos2,5° – cos45°)- R₃·(cos2,5°– cos90°)=0

Отсюда выводим

Принимаем наибольшее значение = 700 м.

Условие минимального радиуса выполняется.

После определения значения радиуса R₃ его необходимо сравнить по формуле (9) т.е. радиус R₃ должен быть больше наибольшего из допустимых радиусов кривизны бокового ствола. Если данное условие не соблюдается, то необходимо произвести корректировку параметров проектного профиля.

7 Определение высоты опорно – ликвидационного цементного моста

Высота цементного моста, определяется по формуле:

Н_м=Н₁+Н₀ , (11)

Н_м= 19,5 + 0,84 = 20,34 м

где Н₁ – высота верхней части моста, м;

Н₀ – высота нижней части моста, м.

Высота верхней части моста, определяется по формуле:

, (12)

где D_бс – диаметр бокового ствола, м;

R₂ – радиус кривизны участка забуривания бокового ствола, м.

Высота нижней части цементного моста, определяется по следующим формулам:

, (13)

где Q_м – ожидаемая суммарная осевая нагрузка на мост, кН (осевая нагрузка от веса буровой колонны);

Q_M = 59,5*1520 = 90345 Н,

D_с – диаметр скважины в которой проводятся работы, м;

[𝜏_м] – удельная несущая способность моста, величина которой определяется как адгезионными свойствами тампонажного материала, так и способом установки моста, МПа (см. таблицу 3)

, (14)

где P_м – максимальная величина перепада давления, действующая на мост при его эксплуатации, МПа;

[△P] – допустимый градиент давления прорыва флюида по зоне контакта моста со стенкой скважины, который определяют в зависимости от способа установки моста и применяемых тампонажных материалов, МПа (см. таблицу 4)

Таблица 3 – Значения допустимых касательных напряжений для обеспечения необходимой несущей способности моста в обсаженной скважине

Способ установки моста	[𝜏м], МПа
С применением скребков и моющих буферных жидкостей на водной основе	1,0
С применением моющих буферных жидкостей	0,5
Без скребков и моющих жидкостей	0,05

Таблица 4 – Значение допустимых градиентов давления при определении высоты цементного моста

Способ установки моста	[△P], МПа/м
С применением скребков и моющих буферных жидкостей на водной основе	5,0
С применением моющих буферных жидкостей	2,0
Без скребков и моющих жидкостей	1,0

Максимальная величина перепада давления, действующая на мост, определяется по формуле:

P_м=P_пл – P_ст , (15)

P_м= 22 – 17,8 = 4,2 м

где P_пл – пластовое давление в существующей скважине, МПа;

P_ст – гидростатическое давление столба бурового раствора, МПа.

Из уравнений (14) и (15) выбирается большее значение H₀ и подставляется в уравнение (11). Подсчитанное по уравнению (11) значение высоты цементного моста и будет являться искомой величиной.